Объекты алгоритмов. Команда присваивания

Вопросы занятия:

·                   Команда присваивания;

·                   Применение команды присваивания при записи алгоритмов;

·                   Свойства присваивания.

 Команда присваивания является одной из основных команд в алгоритмах работы с величинами. То есть величина получает своё значение путём выполнения команды присваивания.

Операция присваивания обозначается знаком двоеточие равно, произносится – присвоить и записывается следующим образом: имя переменной присвоить выражение.

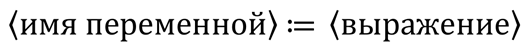
Здесь понятие выражение задаёт порядок выполнения действий над данными и может включать в себя переменные, константы всех типов, знаки операций, стандартные функции, круглые скобки.

Например,

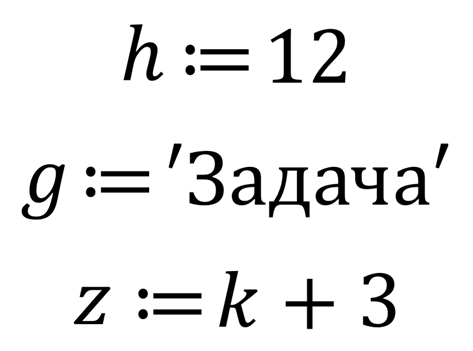
Давайте разберёмся, что означает запись

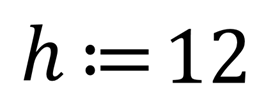
Данную запись можно пояснить так:

В ящик с надписью h надо положить двенадцать, например, мячей. После выполнения этой команды h=12.

То есть команда m:=n означает, что мы должны присвоить переменной m такое же значение, какое имеет величина n, при этом значение второй величины n не изменится.

Нельзя путать знак присваивания со знаком равенства, так, например, при выполнении следующей команды присваивания z:=z+1, величина z станет равной предыдущему значению z, увеличенному на 1. Ясно, что использование в этой записи знака равенства недопустимо, так как никакое z не равно z+1.

Выбор символа присваивания является поводом для споров программистов. Так как использование знака равно для присвоения их запутывает. В результате чего возникает сложный вопрос о выборе символа для оператора сравнения.

Так, Никлаус Вирт утверждал:

Общеизвестно плохим примером является выбор знака равенства для обозначения присваивания. Эта спорная идея опровергает вековую традицию использования знака равно для обозначения равенства двух величин, или высказываний, принимающих значения «истина» или «ложь».

Реализацией этой позиции Вирта можно считать то, что в языке Паскаль, автором которого он является, и который вы будете изучать, оператором присваивания является двоеточие равно, в то время как для сравнения используется просто равно.

Теперь разберёмся с основными свойствами команды присваивания.

Рассмотрим пример. Нам необходимо заполнить таблицу и выяснить чему равны начальные и конечные значения переменных а и b.

Итак, первая команда а :=1. Значит значение переменной а=1 стало равным единице. Переменной b пока не присвоено значения, поэтому она остаётся неопределённой.

Эта особенность является первым свойством присваивания.

То есть, пока переменной не присвоено значение, она остаётся неопределённой;

Заполним следующую строку. Здесь присваивается значение переменной b. Значение, присвоенное переменной а, сохраняется пока не выполнится следующее присваивание, поэтому записываем 1;

Эта особенность является вторым свойством присваивания.

То есть, значение, присвоенное переменной, сохраняется вплоть до выполнения следующего присваивания этой переменной нового значения;

Переменной b:=2*1. То есть значение переменной b=2.

Заполним следующую строку. Переменной а присваиваем значение переменной b. Значение b=2, следовательно, а =2.

Эта особенность является третьим свойством присваивания.

То есть, новое значение, присвоенное переменной, заменяет её предыдущее значение.

Значение переменной b по второму свойству сохраняется. При заполнении последней строки сохраняется значение переменной а.

Переменной b:=a+b. a=2  и b=2. Получаем значение b=4.

В задании необходимо было выяснить, чему равны начальные и конечные значения переменных а и b. Начальное значение переменной а =1, а переменной b=2. Конечные значения, которые получают переменные а и b, соответственно равны 2 и 4.

Таким образом основные особенности команды присваивания таковы:

1. Пока переменной не присвоено значение, она остаётся неопределённой;

2. Значение, присвоенное переменной, сохраняется вплоть до выполнения следующего присваивания этой переменной нового значения;

3. Новое значение, присвоенное переменной, заменяет её предыдущее значение.

Рассмотрим последовательность выполнения команды присваивания:

в первую очередь вычисляется значение выражения, затем результат вычисления присваивается переменной, стоящей слева от знака присваивания.

Например, пусть начальное значение переменной k=1.

После вычисления значения выражения мы присваиваем переменной k:=24,5.

Также важно отметить что, необходимо чтобы тип выражения был совместим с типом соответствующей переменной.

Перейдём к практической части урока.

Первое задание. Необходимо определить, чему станет равна величина k, после выполнения следующего ряда присвоений:

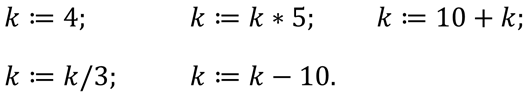
Итак, после выполнения первой команды присваивания k=4. После выполнения второй команды k=20, после третьей k=30, четвёртой – k=10 и пятой – k=0.

То есть, обратите внимание, после присваивания величине нового значения старое забывается.

Следующее задание. Необходимо ответить на вопрос: какое минимальное количество промежуточных переменных потребуется для того, чтобы переменной k было присвоено значение переменной m, переменной m — значение переменной n, а переменной n — значение переменной k? И записать соответствующий алгоритм на алгоритмическом языке.

Для того чтобы правильно решить данную задачу воспользуемся аналогией. Пусть имеются три коробки оранжевого, голубого и зелёного цвета. В этих коробках лежат шарики. В оранжевой коробке лежат шарики зелёного цвета, в голубой коробке лежат шарики оранжевого цвета, а в зелёной коробке – шарики голубого цвета. Необходимо переложить шарики так, чтобы цвета совпали.

Для того чтобы переложить шарики правильно, необходима дополнительная коробка. Тогда можно поступить следующим образом.

Пересыпаем голубые шарики из зелёной коробки в дополнительную. Теперь мы можем пересыпать зелёные шарики из оранжевой коробки в зелёную коробку.

Следующий шаг. Пересыпаем оранжевые шарики из голубой коробки в оранжевую коробку. И последний шаг. Пересыпаем голубые шарики из дополнительной коробки в голубую коробку.

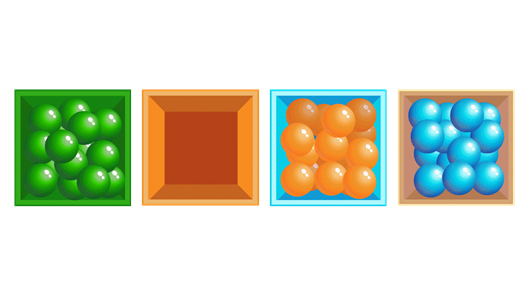
Обратите внимание, для решения данной задачи достаточно было взять одну дополнительную коробку и больше не нужно.

То есть для того чтобы поменять значения трёх величин достаточно ввести одну дополнительную величину.

Для решения нашей задачи введём промежуточную переменную z. Тогда запишем алгоритм обмена значениями k, m и n.

В результате переменной k присвоено значение переменной m, переменной m — значение переменной n, а переменной n — значение переменной k и для этого достаточно ввести одну промежуточную переменную.

Пришло время подвести итоги урока.

Сегодня на уроке мы с вами выяснили, что

Команда присваивания является одной из основных команд в алгоритмах работы с величинами. То есть величина получает своё значение путём выполнения команды присваивания.

Рассмотрели последовательность выполнения команды присваивания

На примере разобрались с основными свойствами команды присваивания.

А также составили алгоритм, в результате которого переменные a, b и c литерного типа обменялись своими значениями.