Вопросы занятия:
· Выражение;
· Правила для записи выражений на алгоритмическом языке;
· Арифметические, логические, строковые выражения.
Мы уже знаем, что данные можно записывать в переменные, которые бывают целыми либо вещественными. Над переменными целого и вещественного типов можно выполнять операции: сложение, вычитание, умножение, деление.
Такое построение называется выражением.
Самыми простыми выражениями будут выражения, которые состоят или из одной переменной или из одной константы.
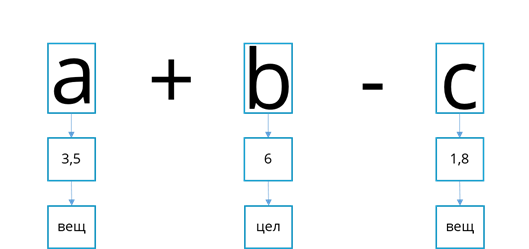
То есть Выражение — это языковая конструкция для поиска значений с помощью операндов.
Итак, как мы уже выяснили, выражения состоят из операндов (констант, переменных, функций), которые объединяются знаками операций.
То есть выражение задаёт порядок выполнения действий над величинами.
Запись алгоритмических выражений имеет свои синтаксические правила. Например, невозможно записывать выражения в виде обыкновенных дробей. Запись пять восьмых компьютер не поймёт. Из математики известно, что черту дроби можно заменить знаком деления.
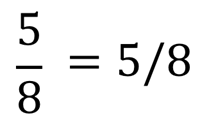
Запись четыре ас компьютер также не поймёт, операцию умножения опускать нельзя: следует писать:
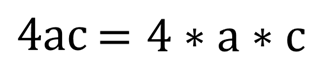
Выполнение каждой операции в выражениях происходит с учётом её приоритета. Порядок выполнения операций следующий:
• Выражения в скобках вычисляются в первую очередь.
• После вычисления значений выражений в скобках вычисляются функции.
• После функций выполняется умножение и деление (они имеют одинаковый приоритет и выполняются в порядке их следования слева направо).
• Далее выполняется сложение и вычитание в порядке их следования.
Выражения делятся на: арифметические, логические и строковые.
Рассмотрим подробнее каждую группу выражений.
Арифметические выражения используются для определения числового значения.
Например,
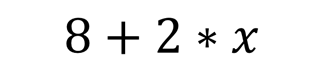
является арифметическим выражением, его значение при
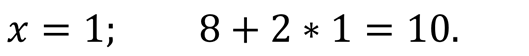
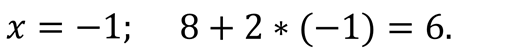
Выражение sqrt (x) служит для обозначения операции извлечения квадратного корня из x. Выражение abs(x) вычисляет модуль значения переменной x, а sqr(x) вычисляет квадрат значения переменной x.
Логические выражения описывают некоторые условия, которые могут удовлетворяться или не удовлетворяться.
Логическое выражение может принимать одно из двух значений - ИСТИНА или ЛОЖЬ. Например,
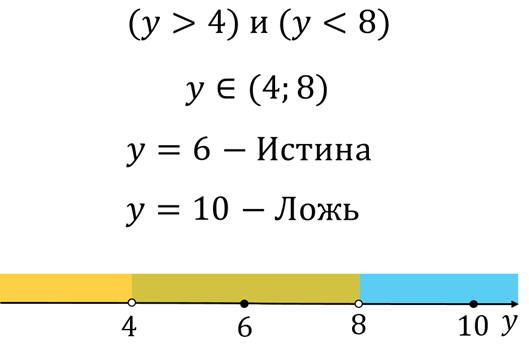
Строковые выражения состоят из величин (констант, переменных) символьного и литерного типов, соответствующих функций и операций сцепления (присоединения).
Операция сцепления обозначается знаком плюс. С помощью данной операции можно соединить несколько последовательностей символов в одну последовательность.
Значениями строковых выражений являются последовательности символов. Например, если строковая величина B = ‘рог’, то значение строкового выражения ’пи' плюс B будет пирог.
Перейдём к практической части урока.
Необходимо записать на алгоритмическом языке и найти значение данного выражения:
Итак,
Запишем сначала данное выражение в алгоритмическом виде.
Вещественные числа записываются в виде десятичной дроби, состоящей из целой и дробной частей, разделённых запятой.
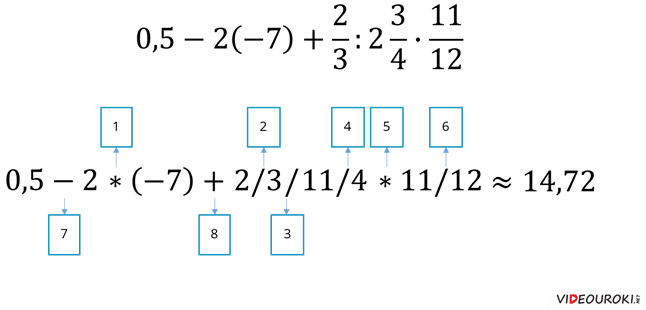
Рассмотрим следующее выражение:
Итак, запишем его сначала на алгоритмическом языке.
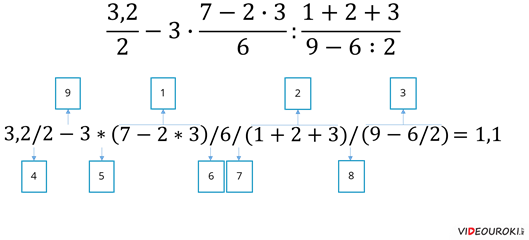
Рассмотрим выражение, содержащее функции. Запишем на алгоритмическом языке и найдём его значение.
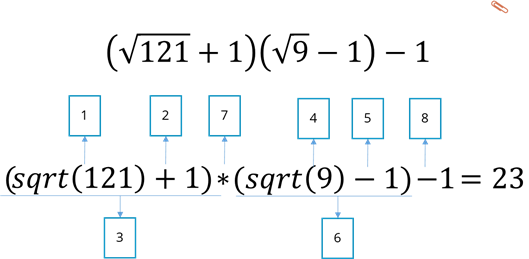
Рассмотрим следующий пример.
Необходимо изобразить в декартовой прямоугольной системе координат область, в которой и только в которой истинно следующее логическое выражение:
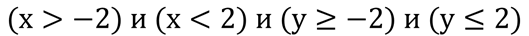
Обратите внимание, поскольку логическое выражение содержит союз И, то оно будет истинно только тогда, когда будет истинно каждое из выражений из которых оно состоит.
Также необходимо отметить что, поскольку третье и четвёртое неравенства нестрогие, то в окончательное решение будут входить точки, которые лежат на этих отрезках.
Итак, изобразим декартовую систему координат. Отметим на оси ОX точку -2. Проведём прямую, параллельную оси ОY. Решениями первого неравенства будут те точки координатной плоскости, которые принадлежат выделенной области. У этих точек первая координата будет больше -2.
Для решения второго неравенства, отметим на оси ОX точку с координатой 2. Решениями второго неравенства будут те точки координатной плоскости которые принадлежат выделенной области. У этих точек первая координата будет меньше 2.
Решая аналогично третье и четвёртое неравенство получим, что решениями логического выражения будут точки расположенные в выделенной области.
Давайте проверим. Возьмём точку, принадлежащую выделенной области, например, точку с координатами (1, 1).
Подставим координаты в наше логическое выражение и проверим каждое неравенство. Все неравенства принимают истинное значение.
По определению логическое выражение содержащее союз И, будет истинно только тогда, когда будет истинно каждое из выражений из которых оно состоит. Следовательно всё выражение принимает истинное значение.
Теперь возьмём точку, не входящую в выделенную область. Например, точку с координатами (-4, -1).
Подставим координаты в наше логическое выражение и проверим каждое неравенство. Первое неравенство принимает значение ложь, остальные неравенства принимают значение истина.
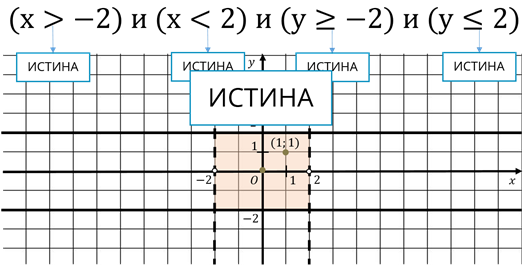
По определению логическое выражение содержащее союз И, будет истинно только тогда, когда будет истинно каждое из выражений из которых оно состоит. Следовательно всё выражение принимает значение Ложь.
Пришло время подвести итоги урока.
Выражение — это языковая конструкция для поиска значений с помощью операндов.
Запись алгоритмических выражений имеет свои синтаксические правила.
Выполнение каждой операции в выражениях происходит с учётом её приоритета. Порядок выполнения операций следующий:
• Выражения в скобках вычисляются в первую очередь.
• После вычисления значений выражений в скобках вычисляются функции.
• После функций выполняется умножение и деление (они имеют одинаковый приоритет и выполняются в порядке их следования слева направо).
• Далее выполняется сложение и вычитание в порядке их следования.
Выражения делятся на: арифметические, логические и строковые.

 Получите свидетельство
Получите свидетельство Вход
Вход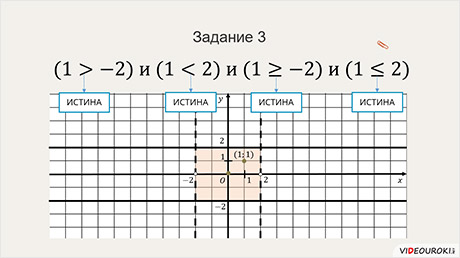




 5998
5998

