Квадратный корень из степени

Прежде чем преступать к изучению новой темы, давайте вспомним определение модуля числа.

Итак, модулем числа а называют расстояние (в единичных отрезках) от начала координат до точки А (а).

Также модулем положительного числа называется само это число.

Модуль числа нуль равен нулю.

А модулем отрицательного числа называется противоположное ему число.

Задание: найти значение выражения , при  и при .

Легко заметить, что в первом примере в ответе тоже получается . Обратите внимание, в каждом из рассмотренных примеров, корень из квадрата числа равен модулю этого числа.

Теорема: При любом значении х верно равенство:

Следовательно, При любом  значение выражения  совпадает со значением выражения .

Равенство  является тождеством.

Это тождество применяется при извлечении квадратного корня из степени с чётным показателем. Чтобы извлечь корень из степени с чётным показателем, достаточно представить подкоренное выражение в виде квадрата некоторого выражения и воспользоваться тождеством: .

Например: преобразуем выражения:

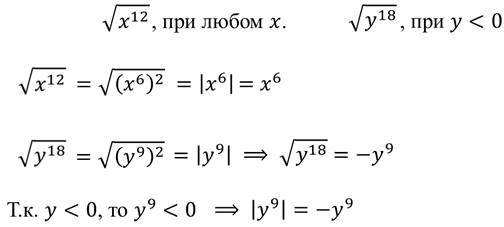
Задание 2: найдите значение выражения.

Итоги:

При любом значении икс верно равенство: .

Это равенство является тождеством и применяется при извлечении квадратного корня из степени с чётным показателем.

Чтобы извлечь корень из степени с чётным показателем, достаточно представить подкоренное выражение в виде квадрата некоторого выражения и воспользоваться тождеством: .