Получите свидетельство
Вход
Для начала давайте вспомним определение арифметического квадратного корня. Итак, арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а.
Пример 1:
Пример 2:
Следует обратить внимание, что
Заметим, что
Видно, что квадратный корень из произведения двух неотрицательных чисел равен произведению квадратных корней из этих чисел.
Этим свойством обладает квадратный корень из произведения любых двух неотрицательных чисел.
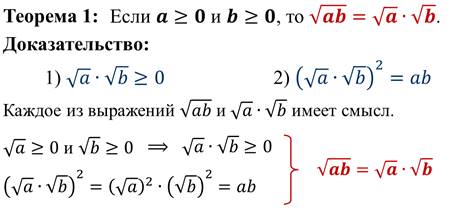
Чтобы извлечь квадратный корень из произведения неотрицательных чисел, можно извлечь его из каждого сомножителя отдельно и результаты перемножить.
Следует заметить, что это свойство распространяется и на тот случай, когда подкоренное выражение представляет собой произведение трёх, четырёх и т.д. неотрицательных множителей.
Например:
Корень из неотрицательных множителей равен произведению корней из этих множителей.
Верно и обратное утверждение: произведение корней из неотрицательных чисел равно корню из произведения этих чисел.
Задание: вычислите значение выражения.
Решение:
Рассмотрим теперь арифметический квадратный корень из дроби.
Пример 1:
Видим, что квадратный корень из дроби равен корню из числителя, делённому на корень из знаменателя.
Этим свойством обладает квадратный корень из дроби, числитель которой неотрицательное число, а знаменатель положителен.
Чтобы извлечь квадратный корень из дроби, можно извлечь корень отдельно из числителя и знаменателя и первый результат разделить на второй.
Вывод: корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, деленному на корень из знаменателя.
Верно и обратное утверждение: частное корней равно корню из частного этих чисел.
Выполнить задание: вычислите значение выражения.
Решение:
Итоги:
Корень из неотрицательных множителей равен произведению корней из этих множителей.
Корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, деленному на корень из знаменателя.
0
24894
