Ранее вы познакомились с функцией у = х2 и научились строить её график, который имеет особое название – парабола. Сегодня эта функция нам пригодится для изучения нового материала.

Пусть есть некоторый квадрат с длиной его стороны а см и площадью S см2.

Тогда, подставляя указанные данные в формулу
площади квадрата, имеем  .
Причём, известно, что
.
Причём, известно, что  ,
т.к. длина это неотрицательная величина. Эта формула выражает
зависимость площади квадрата от длины его стороны. Т.е. каждому значению длины а
стороны квадрата соответствует единственное значение его площади S.
,
т.к. длина это неотрицательная величина. Эта формула выражает
зависимость площади квадрата от длины его стороны. Т.е. каждому значению длины а
стороны квадрата соответствует единственное значение его площади S.
А теперь давайте выразим из формулы площади квадрата формулу для нахождения длины стороны квадрата.
Т.е.  .
.
Эта формула выражает зависимость длины стороны квадрата от его площади. Получаем, что для каждого значения площади S можно указать соответствующее ему единственное значение длины стороны а.
Формулами

задаются функциональные зависимости между одними и теми же переменными. Только в первом случае независимой переменной является длина а стороны квадрата, а во втором – площадь S квадрата.
Давайте заменим в каждой из формул независимую переменную буквой х, а зависимую переменную буквой у. Тогда формулы примут вид:

Построим графики этих функций.
Графиком функции  ,
является парабола.
,
является парабола.

Но у нашей функции, обратите внимание, есть
очень важная оговорка:  ,
а значит, графиком нашей функции будет лишь часть параболы – её правая ветвь.
,
а значит, графиком нашей функции будет лишь часть параболы – её правая ветвь.

Теперь нужно построить график функции  .
.
Для этого зададим несколько значений аргументу
х и вычислим соответствующие значения функции. Обратите внимание, будем
задавать только неотрицательные значения х, т.к. при  выражение
выражение
 не
имеет смысла.
не
имеет смысла.


Итак, мы с вами составили таблицу значений функции. Теперь давайте отметим в координатной плоскости найденные точки. Затем соединим их линией.

Получили график функции  .
.
Из рисунка видно, что график функции  лишь
один раз касается оси Оу, в точке с координатами (0; 0).
лишь
один раз касается оси Оу, в точке с координатами (0; 0).
Как видно, график напоминает повернутую параболу, точнее одну из её ветвей. Теперь стоит отметить некоторые из свойств, которыми обладает данная функция.
Как мы уже заметили, график функции  ,
как и график функции
,
как и график функции  ,
где
,
где  ,
представляет собой ветвь параболы.
,
представляет собой ветвь параболы.
Эти графики симметричны относительно прямой  .
.

Доказательство симметрии графиков основано на
том, что точки с координатами (а, b) и (b, а) симметричны относительно прямой  .
.
Докажем симметричность наших графиков.
Пусть есть две точки: точка M (a, b)
и некоторая точка N (b,
a). И пусть точка M
принадлежит графику функции  ,
где
,
где  .
Подставим координаты точки M в формулу
.
Подставим координаты точки M в формулу  .
Тогда верно равенство
.
Тогда верно равенство  .
По условию а – неотрицательное число. Значит, можно вычислить а, тогда
.
По условию а – неотрицательное число. Значит, можно вычислить а, тогда  .
Теперь подставим координаты точки N в формулу
.
Теперь подставим координаты точки N в формулу  .
Тогда верно равенство
.
Тогда верно равенство  .
Т.е. точка N (b, a) принадлежит графику функции
.
Т.е. точка N (b, a) принадлежит графику функции  .
.
Верно и обратное: если некоторая точка принадлежит второму графику, то точка, у которой координатами являются те же числа, но взятые в другом порядке, принадлежит первому графику.
Вывод:
Каждой точке M (a, b) графика функции  ,
где
,
где  ,
соответствует точка N (b,
a) графика функции
,
соответствует точка N (b,
a) графика функции  и
наоборот.
и
наоборот.
Т.к. точка M (a, b) и точка N (b, a)
симметричны относительно прямой  ,
то и сами графики симметричны относительно этой прямой.
,
то и сами графики симметричны относительно этой прямой.
Задание 1:
с помощью графика функции  найдите
значение аргумента, которому соответствует значение функции:
найдите
значение аргумента, которому соответствует значение функции:  .
.
Решение:

Задание 2: функция задана
формулой  .
Определите значение функции при
.
Определите значение функции при  .
.
Решение:

Задание 3: принадлежат ли графику
функции  точки
точки
 ,
,
 и
и
 .
.
Решение:

Итоги:
График функции  имеет
вид:
имеет
вид:

График функции  обладает
такими свойствами:
обладает
такими свойствами:
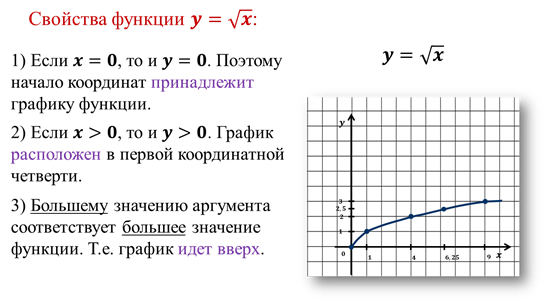
1) Если  ,
то и
,
то и  .
Поэтому начало координат принадлежит графику функции.
.
Поэтому начало координат принадлежит графику функции.
2) Если  ,
то и
,
то и  .
График расположен в первой координатной четверти.
.
График расположен в первой координатной четверти.
3) Большему значению аргумента соответствует большее значение функции. Т.е. график идёт вверх.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 7665
7665

