Вы уже научились находить значения некоторых квадратных корней. Например, таких как:

Но бывает так, что необходимо найти квадратный корень из числа, который уже нельзя так сходу определить. Тогда приходят к нахождению приближённых значений квадратного корня.
Например:
Надо найти  .
.
До этого мы с вами уже говорили, что нет такого целого числа, квадрат которого бы равнялся двум.
Обратимся к параболе.

Прямая  пересекает
параболу в двух точках. Абсцисса первой точки расположена между числами -1 и -2,
абсцисса второй точки между числами 1 и 2.
пересекает
параболу в двух точках. Абсцисса первой точки расположена между числами -1 и -2,
абсцисса второй точки между числами 1 и 2.
А т.к. нас интересует арифметический квадратный корень, то рассматриваем только точку в первой координатной четверти (т.е. с положительной абсциссой). По рисунку можно лишь сказать, что значение корня из двух расположено между числами 1 и 2.
Попробуем все же вычислить приближённое
значение  с
двумя знаками после запятой. Будем рассуждать следующим образом:
с
двумя знаками после запятой. Будем рассуждать следующим образом:
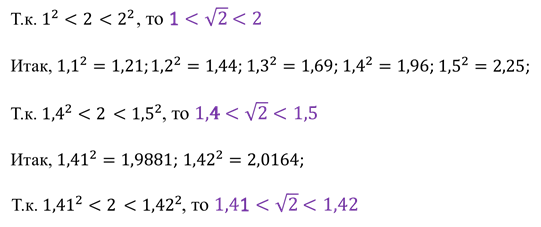
Т.к. нужно вычислить  с
точностью до двух знаков после запятой, то мы можем уже остановиться и не
продолжать вычисления дальше. Поэтому имеем
с
точностью до двух знаков после запятой, то мы можем уже остановиться и не
продолжать вычисления дальше. Поэтому имеем

Это и будет ответом. Если бы необходимо было вычислить ещё более точное значение, нужно было бы продолжать вычисления, повторяя снова и снова цепочку рассуждений. Данный приём позволяет извлекать арифметический квадратный корень с любой точностью.
Можно показать наши рассуждения относительно
значения  на координатной прямой.
на координатной прямой.
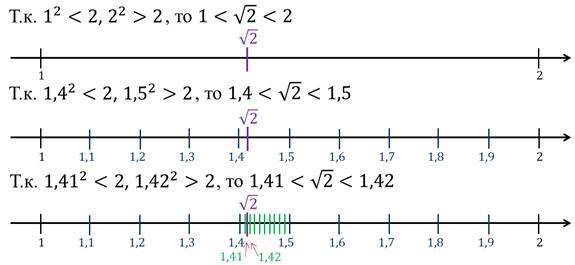
В первом шаге показано, что значение  расположено между числами 1 и 2.
расположено между числами 1 и 2.
Во втором шаге нашли значение корня с точностью до десятых. И пришли к выводу, что это значение заключено между числами 1,4 и 1,5.
Затем, в третьем шаге показано, что значение  расположено
между числами 1,41 и 1,42 с точностью до сотых. И т.д..
расположено
между числами 1,41 и 1,42 с точностью до сотых. И т.д..
В практических расчётах для нахождения приближённых значений квадратных корней используют специальные таблицы или вычислительную технику.

Рассмотрим, как можно находить значения квадратных корней с помощью калькулятора.
Для этого используют клавишу, на которой изображён знак квадратного корня. Чтобы извлечь корень из некоторого числа, нужно ввести это число в калькулятор. Пауза нажать клавишу со знаком корня. И на экране высветится приближённое значение корня.
Убедимся в правильности работы калькулятора. Сначала давайте попробуем найти значение корня, которого вы уже помните наизусть.
Например:
Нужно найти значение  .
Конечно, вы с ходу скажите, что оно равно 5. Проверим. Вводим в калькулятор
число 25, затем нажимаем волшебную клавишу со знаком корня и
видим… значение равно 5.
.
Конечно, вы с ходу скажите, что оно равно 5. Проверим. Вводим в калькулятор
число 25, затем нажимаем волшебную клавишу со знаком корня и
видим… значение равно 5.
Проверим, правильно ли мы рассуждали
относительно значения  .
Вводим число 2 в калькулятор, нажимаем клавишу с корнем и видим
такие цифры: 1, запятая, 4, 1 и дальше ещё много циферок. Обратите внимание, получили
бесконечную непериодическую дробь, т.е. значение
.
Вводим число 2 в калькулятор, нажимаем клавишу с корнем и видим
такие цифры: 1, запятая, 4, 1 и дальше ещё много циферок. Обратите внимание, получили
бесконечную непериодическую дробь, т.е. значение  –
иррациональное число. Но т.к. нам нужно было найти приближённое
значение
–
иррациональное число. Но т.к. нам нужно было найти приближённое
значение  с
точностью до сотых, то мы убедились, что
с
точностью до сотых, то мы убедились, что  .
.
Задание:
Сравните числа.
Решение:


 Получите свидетельство
Получите свидетельство Вход
Вход




 0
0 30105
30105

