Получите свидетельство
Вход
Рассмотрим уравнение 
, где а – произвольное число.
В зависимости от числа а при решении этого уравнения возможны три случая.
1 случай:
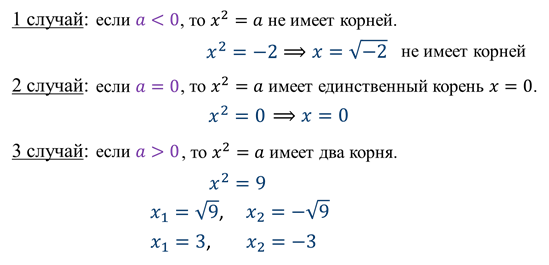
Давайте убедимся в этом. В курсе 7-ого класса
вы познакомились с замечательной функцией 
и
научились строить её график, который называется параболой.
Прямая у = а при а > 0 пересекает параболу в двух точках. Обозначим абсциссы точек пересечения х1 и х2.
Вернёмся к уравнениям, которые решали ранее.
Покажем это решение на графике.
Задание 1: найти корни уравнений.
Вообще, при любом 
уравнение
имеет
неотрицательный корень 
.
Какое бы число 
мы
бы ни взяли, всегда найдётся неотрицательное число, квадрат которого равен 
.
Выражение имеет
смысл при любом .
Задание 2: найти корни уравнений.
Решение:
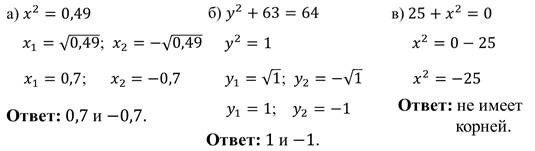
Итоги:
При решении уравнения 
возможны три случая, в зависимости от числа а:
1) если а < 0, то уравнение не
будет иметь корней.
2) если а = 0, то уравнение имеет единственный корень, который равен 0.
3) если а > 0, тогда уравнение имеет два корня.
0
28976
