На этом уроке мы познакомимся с новыми для вас понятиями такими, как квадратные корни и арифметический квадратный корень. А также научимся находить значения корней.
Задача: мама выделила Маше для клумбы участок земли квадратной формы. Площадь этого участка 100 м2. Определите длину стороны участка.
Решение:

Числа 10 и минус 10 называют квадратными
корнями уравнения 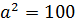 .
.
Определение
Квадратным корнем из числа а называют число, квадрат которого равен а.
Вернёмся к задаче. Мы знаем, что длина – это положительная величина. А значит, корень второго уравнения – минус 10, не подходит. И тогда длина стороны Машиной клумбы равна 10 метрам.
Решая данную задачу, мы с вами столкнулись с неоднозначностью: получили два корня, но к решению задачи подошел только один. И чтобы не было проблем с выбором корня вводят понятие арифметического квадратного корня.
Определение:
Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а.
Обратите внимание, в определении прозвучала фраза «неотрицательное число». Почему нельзя сказать просто … «положительное число»? … Потому что квадрат нуля, есть само число нуль. А оно, как вы знаете, не является ни положительным числом, ни отрицательным. Поэтому и используют термин «неотрицательное число».
Арифметический квадратный корень из числа а обозначают так:
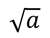
Знак 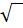 называют
знаком арифметического квадратного корня или знаком радикала (от
латинского слова «радикс» – корень).
называют
знаком арифметического квадратного корня или знаком радикала (от
латинского слова «радикс» – корень).
Выражение, стоящее под знаком корня называют подкоренным выражением.
При чтении записи, слово «арифметический» не произносят, а читают просто «квадратный корень из а».
Операцию нахождения арифметического квадратного корня из числа, называют извлечением корня.
Рассмотрим несколько примеров извлечения корня из числа. Итак, найдём значения корней.
Решение:
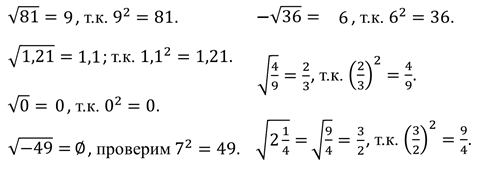
Запомните, квадратный корень можно извлекать только из неотрицательных чисел.

При 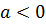 выражение
выражение
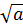 не
имеет смысла. Т.к. нет такого числа квадрат, которого бы был
отрицательным числом.
не
имеет смысла. Т.к. нет такого числа квадрат, которого бы был
отрицательным числом.
Из определения арифметического
квадратного корня следует, что при любом а, при котором выражение 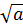 имеет
смысл, верно равенство
имеет
смысл, верно равенство 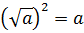 .
.
Задание 1: найдите число, арифметический квадратный корень из которого равен: 1; 4; 0,3.
Решение:
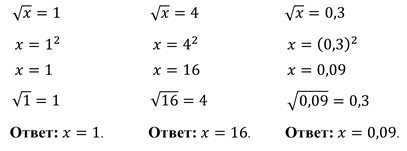
Задание 2: найдите значение выражения.
Решение:
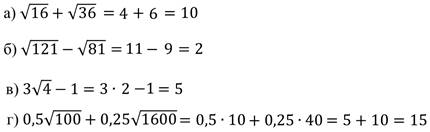
Итоги:
Квадратным корнем из числа а называют число, квадрат которого равен а.
Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а.
Операцию нахождения арифметического квадратного корня из числа, называют извлечением корня.
Равенство 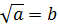 верно,
когда выполняются два условия:
верно,
когда выполняются два условия:
1) 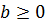 и 2)
и 2) 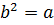
При 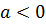 выражение
выражение
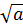 не
имеет смысла.
не
имеет смысла.
Из определения арифметического квадратного
корня следует, что при любом а, при котором выражение 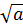 имеет
смысл, верно равенство
имеет
смысл, верно равенство
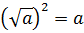

 Получите свидетельство
Получите свидетельство Вход
Вход




 1
1 10136
10136


ОТЛИЧНЫЙ КОНСПЕКТ СОДЕРЖАНИЯ МАТЕРИАЛА, ОЧЕНЬ КОМПЕТЕНТНО СОСТАВЛЕН