Упрощение выражений

На этом уроке мы познакомимся с распределительным свойством умножения. А также научимся при помощи него упрощать выражения.

На предыдущих уроках мы с вами изучили переместительное и сочетательное свойства сложения и умножения.

Давайте запишем эти свойства в буквенной записи.

Переместительное свойство сложения:

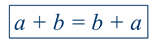
Сформулируем его: от перемены мест слагаемых сумма не меняется.

Это же свойство, но для действия умножения:

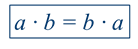
Его формулировка: от перемены мест множителей произведение не меняется.

А теперь запишем буквенные записи сочетательного свойства сложения и умножения.

Для сложения:

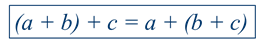
Чтобы к числу прибавить сумму двух чисел, мы можем сначала прибавить к этому числу первое слагаемое, а потом к полученной сумме второе слагаемое.

Это же свойство, но для умножения:

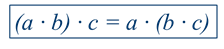
Чтобы число умножить на произведение двух чисел, мы можем сначала умножить это число на первый множитель, а потом полученное произведение на второй множитель.

Не трудно заметить, что эти свойства одинаковые, но каждое из них закреплено за определённым действием. Сегодня мы познакомимся со свойством, которое одновременно относится и к умножению и к сложению.

Задача

В магазин привезли 4 коробки с карандашами. В каждой коробке по 16 упаковок цветных карандашей и по 12 упаковок простых карандашей. Сколько всего упаковок карандашей привезли в магазин?

Решение: Эту задачу можно решить несколькими способами.

1-ый способ:

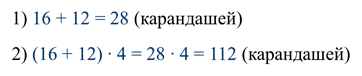
А можно решить вторым способом:

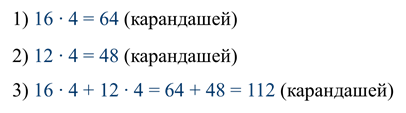
Так как количество упаковок карандашей не зависит от способа, каким оно подсчитывается, то выражения, которые мы получили для решения задачи, равны:

Если вместо чисел 16, 12 и 4 мы возьмём любые натуральные числа a, b и c, то получим равенство:

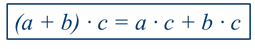
Свойство чисел, выраженное этим равенством, называется распределительным свойством умножения относительно сложения.

Его можно сформулировать так: для того чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить получившиеся произведения.

Распределительное свойство верно и не только для двух слагаемых, но и для любого количества слагаемых.

Пример

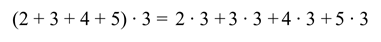
Распределительное свойство умножения действует и относительно вычитания. В буквенном виде записывают его так:

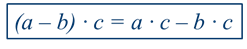
А звучит оно так: для того чтобы умножить разность на число, можно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе.

Пример

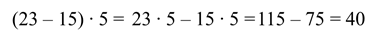
Когда мы читаем равенство слева на право, т.е. переходим от произведения к сумме, то говорим, что раскрываем скобки.

Перепишем это равенство справа налево. Когда мы переходим от суммы к произведению, то говорим, что выносим общий множитель за скобки. Аналогично и для распределительного свойства умножения относительно вычитания.

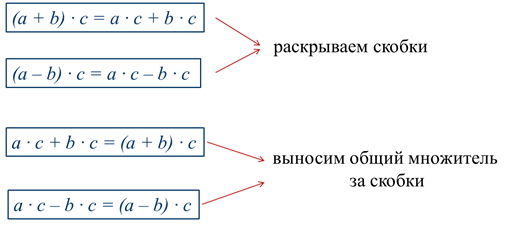
С помощью распределительного свойства очень удобно упрощать выражения. Переместительное свойство умножения позволяет менять местами множители. Поэтому безразлично, где стоит множитель с – перед скобкой или после неё.

Примеры

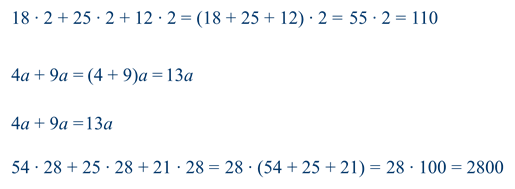
Также удобно пользоваться распределительным свойством умножения при решении уравнений.

Пример

Решим уравнение:

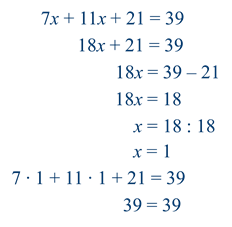
При упрощении выражений используют и сочетательное свойство умножения.

Пример

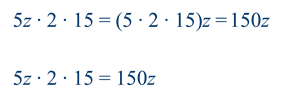
Итоги

Итак, сегодня на уроке мы познакомились с распределительным свойством умножения относительно сложения и вычитания, а также научились при помощи их упрощать выражения.