Топология является одним из самых «молодых» разделов геометрии. Он изучает свойства фигур и тел, которые не изменяются при деформации. Фигуры можно сжимать и растягивать, сгибать и выпрямлять, но нельзя разрезать и склеивать.
Эта ветвь математики начала развиваться с того момента, как в середине девятнадцатого века немецкий математик и астроном Август Фердинанд Мёбиус обнаружил существование удивительного одностороннего листа бумаги.
Топология в основном изучает поверхности тел и находит математическое родство между предметами, которые, казалось бы, никак между собой не связаны. Например, с точки зрения топологии гайку, макаронину и кружку роднит то, что каждый из этих предметов имеет отверстие, хотя во всех остальных отношениях они совершенно различны.

Эти предметы можно назвать «топологическими родственниками».
Давайте с вами рассмотрим опыт с поверхностями и отверстиями, полученными из бумажной полоски. Возьмём две бумажные полоски. Удобнее всего использовать полоски длиной примерно 30 см и шириной 3 см.
У первой полоски склеим её противоположные концы.
У второй полоски тоже склеим её противоположные концы, но при этом предварительно перевернём один из них.

Эти кольца очень похожи. Но представьте муравья, находящегося на поверхности простого кольца. Удастся ли ему попасть на обратную (изнаночную) сторону кольца, не переползая через край ленты? Конечно же, не получится!
А если муравей будет ползти по перекрученному кольцу?
Давайте проведём непрерывную линию по одной из сторон перекрученного кольца. Линия прошла по обеим сторонам кольца, хотя она была проведена непрерывно.
Это и обнаружил Мёбиус.

Получается, что у перекрученного кольца имеется только одна сторона. Впоследствии его назвали листом Мёбиуса (или лентой Мёбиуса). Позже математики открыли ещё целый ряд односторонних поверхностей. Например, бутылка Клейна – односторонняя поверхность, впервые описанная в 1882 году немецким математиком Феликсом Клейном.

Односторонняя поверхность – лист Мёбиуса – положила начало целому направлению в геометрии. Но по-прежнему привлекает к себе внимание не только учёных, но и людей творческих профессий. Международный символ переработки отходов представляет собой лист Мёбиуса.

Продолжим рассматривать опыты с листом Мёбиуса и подобными ему кольцами.
Возьмём простое кольцо и перекрученное на пол-оборота кольцо (лист Мёбиуса). Разрежем вдоль каждое из них. Разрезав обычное кольцо, у нас получилось два кольца.

При этом длина окружности каждого кольца та же, но кольца в два раза уже.
Разрезав лист Мёбиуса, мы получили кольцо, которое перекручено на два полуоборота, длина его окружности в два раза больше, и кольцо уже исходного в два раза. Хотя казалось бы, что лист должен был распасться.

А вот если взять ленту Мёбиуса шириной 3 см и разрезать её вдоль, отступив от края на 1 см, то получим два кольца – одно большое и сцепленное с ним маленькое. При этом маленькое кольцо – это лента Мёбиуса. Большое представляет собой кольцо, которое перекручено на два полуоборота.

Вы можете провести опыт, который называется «Солдатик-перевёртыш». Вырежьте из бумаги солдатика и отправьте его вдоль пунктира, идущего посередине листа Мёбиуса. В каком виде солдатик вернётся к месту старта?

К топологическим относятся и задачи на вычерчивание фигур одним росчерком. Такие задачи на самом первом занятии. Мы с вами выяснили, что фигуру, изображённую на рисунке, можно нарисовать, не отрывая карандаша от бумаги и не проводя более одного раза никакой линии. Причём начать рисовать фигуру можно с любой вершины.

Также мы привели пример фигуры, которая на первый взгляд проще, так как содержит меньшее количество линий, но вычертить её, не отрывая карандаша от бумаги, не получится.

Почему какие-то фигуры получается нарисовать, не отрывая карандаша от бумаги и не проводя никакую линию дважды, а какие-то нет?
Давайте разберёмся. Посмотрите на рисунок, на котором изображена сеть линий. Она называется графом. «Граф» в переводе с греческого означает «пишу». Точки, в которых соединяются линии, называются узлами.

В нашем графе 5 узлов. При этом в первом, втором и третьем узлах соединяется по две линии, то есть чётное число. Эти узлы называются чётными.
А в четвёртом и пятом узлах соединяется по три линии, то есть нечётное число. Эти узлы называются нечётными.
Получается, что в этом графе 3 чётных узла и 2 нечётных. Данную фигуру можно нарисовать одним росчерком, то есть не отрывая карандаша от бумаги и не проводя никакую линию дважды.

Теперь посмотрите на фигуру, которая представляет собой домик с дверью. Она содержит 9 узлов. Первый, второй, третий, шестой и седьмой узлы являются чётными, а четвёртый, пятый, восьмой и девятый – нечётными. В этом графе 5 чётных узлов и 4 нечётных. Отметим, что нечётных узлов здесь больше 2.

Запомните! Если в фигуре (на графе) число нечётных узлов больше двух, то её нельзя нарисовать одним росчерком.
Получается, что фигуру в виде домика с дверью нельзя нарисовать одним росчерком.
Давайте рассмотрим известную задачу, которая положила начало задачам на вычерчивание фигур одним росчерком. Это задача о «кёнигсбергских мостах». Город Кёнигсберг был расположен на берегах и двух островах реки Преголи. Различные части города были соединены семью мостами.

Среди жителей города была распространена такая загадка: можно ли выбрать такой маршрут, чтобы пройти один и только один раз по каждому мосту, а затем вернуться в начальную точку пути? Многие пытались решить эту задачу как теоретически, так и практически, во время прогулок, но это никому не удавалось.
Леонард Эйлер – выдающийся математик, член Петербургской академии наук в 1736 году заинтересовался этой задачей, и ему удалось её разрешить.
Итак, к восточному острову ведут 3 моста. 3 – число нечётное. Если прогулка начинается вне восточного острова, то поскольку по каждому из трёх мостов надо пройти один раз, заканчиваться она должна на этом острове.
Это можно сравнить с включением и выключением настольной лампы. Будем поочерёдно включать и выключать настольную лампу, нажимая на кнопку. Если вначале лампа была выключена, то после трёх таких операций (включили-выключили-включили) лампа окажется включённой.
Участки суши и мосты обозначим буквами.

К западному острову ведут 5 мостов. 5, как и 3, – число нечётное. Следовательно, если прогулка начинается вне западного острова, то заканчивается она на западном острове.
На южный и на северный берега реки ведут по 3 моста, а значит, и к ним можно применить такие же рассуждения.
Получается, что каждый из четырёх участков суши, обозначенных буквами A, B, C и D, должен быть либо началом, либо концом прогулки. Но это невозможно.
План города для решения этой задачи можно изобразить вот таким графом:

Тогда задача сведётся к вычерчиванию этой фигуры одним росчерком. На этом графе четыре узла (они соответствуют берегам C и B и островам A и D) и семь кривых, которые обозначают мосты a, b, c, d, e, f, g. Все узлы этого графа являются нечётными, так как в каждом из них сходится нечётное число линий.
Если бы существовал искомый маршрут, то эту сеть кривых можно было бы изобразить одним росчерком. Получается, что задача о мостах доказывает, что изображённую фигуру нельзя нарисовать одним росчерком. Так же обосновывается наше правило для любой фигуры.
А сейчас давайте решим задачу. Выясните, какие из фигур можно вычертить, не отрывая карандаша от бумаги и не проводя два раза по одной и той же линии.

Решение.


Решим ещё одну задачу. Выясните, сможет ли пчела последовательно обойти все 12 рёбер куба, не проходя дважды по одному ребру, не подпрыгивая и не перелетая с места на место.
Решение.


 Получите свидетельство
Получите свидетельство Вход
Вход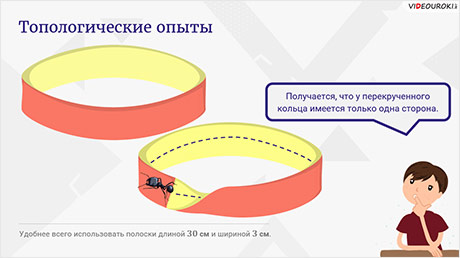




 4665
4665

