Логарифмы

При решении показательных уравнений, мы с вами представляли обе части уравнения в виде степеней с одинаковыми основаниями и рациональными показателями.

Вот, например, при решении уравнения  мы  сначала представляем, как , а потом по свойствам степеней заменяем степенью .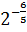

Из равенства степеней с одинаковыми основаниями можем сделать вывод о равенстве показателей. Однако не все уравнения можно решить таким образом.  

Давайте решим уравнение .

Заметим, что это уравнение не получится решить таким же способом, как мы решали предыдущее. Ведь число 3 нельзя представить в виде степени с основанием 2 и рациональным показателем.

Действительно, если бы равенство , где m и n – натуральные числа, было верным, то, возведя его в степень n, мы бы получили верное равенство .

Но ведь последнее равенство неверно, так как левая его часть является чётным числом, а правая – нечётным. А значит, не может быть верным и равенство .

Но ведь с другой стороны, график функции  пересекается прямой y = 3.

А это говорит о том, что уравнение  имеет корень.

В связи с этим возникают два вопроса: «как записать этот корень?» и «как его вычислить?».

Начнём с первого вопроса. И чтобы ответить на него введём определение.

Итак, показатель степени, в которую нужно возвести число а, чтобы получить число , называется логарифмом числа  () по основанию а, где  и отлично от 1. Обозначают его так: , а читают «логарифм числа по основанию а».

Вернёмся к нашему уравнению.

Исходя из определения логарифма, теперь мы можем записать корень нашего уравнения. То есть .

Например, значения следующих логарифмов записывают так:

, так как .

, так как .

 , так как

Заметим, что из определения логарифма вытекает, что его можно найти лишь для положительных чисел, поскольку .

Таким образом, логарифм определён лишь для положительных чисел.

Так почему же в определении логарифма основание берётся только положительным?

Пусть, например, .

В какую степень нужно возвести это число а, чтобы получить, например, 2?

Конечно же, такой степени не существует. Поэтому и рассматривать логарифмы с отрицательным основанием не имеет смысла.

Также не имеет смысла рассматривать и логарифмы по основанию 1. Ведь в какую бы степень мы ни возвели 1, всегда будет получаться 1. Значит, ни у какого числа, кроме 1, не будет логарифма по основанию 1.

Также нужно отметить, что из определения следует, что логарифм одного по любому основанию равен 0.

Равенства  и , в которых  и , , а число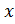 может быть любым, выражают одно и то же соотношение между числами ,  и . Подставив в первое равенство выражение  из второго, получим тождество, которое называют основным логарифмическим тождеством.

Ведь в самом деле, если возвести число а в ту степень, в которую его надо возвести, чтобы получилось число , то получится .

Например,

,

,

.

Действие нахождения логарифма числа называют логарифмированием. Действие нахождения числа по его логарифму называют потенцированием.

Немного из истории. Слово логарифм происходит от слияния двух греческих слов (λόγος и ἀριθμός), которые переводятся как отношение чисел, одно из которых является членом арифметической прогрессии, а другое геометрической. Впервые это понятие ввёл английский математик Джон Непер.

Кроме того, этот человек известен тем, что он первый изобрёл таблицы логарифмов.

В 1614 году Джон Непер опубликовал на латинском языке сочинение под названием «Описание удивительной таблицы логарифмов». В нём было краткое описание логарифмов и их свойств, а также восьмизначные таблицы логарифмов синусов, косинусов и тангенсов. Теорию логарифмов Непер изложил в другой своей книге «Построение удивительной таблицы логарифмов».

Как вскоре обнаружилось, из-за ошибки в алгоритме все значения таблицы Непера содержали неверные цифры после шестого знака. Однако это не помешало новой методике вычислений получить широчайшую популярность, и составлением логарифмических таблиц занялись многие европейские математики.

В 1620 году английский математик Эдмунд Гюнтер для облегчения вычислений предложил механическое устройство, использующее логарифмическую шкалу.

Чуть позже Эдмунд Уингейт и Уильям Отред изобрели первую логарифмическую линейку, которая до появления карманных калькуляторов служила незаменимым расчётным орудием инженеров.

В России первые таблицы логарифмов были изданы в 1703 году при участии Леонтия Филипповича Магницкого.

А теперь давайте приступим к практической части нашего урока.

Задание 1. Найдите значения логарифмов:
а) ;     б) ;     в) ;     г) .

Решение.

Найдём логарифм числа .

Заметим, что , то есть для того чтобы получить число 32, надо 2 возвести в 5-ю степень. Следовательно, .

Далее найдём логарифм .

.

Значит, .

В следующем условии нужно найти логарифм числа .

Для того чтобы получить число , надо . Следовательно,
.

И найдём ещё значение логарифма числа .

 – это .

Значит, .

Задание 2. Найдите : а) ;     б) .

Решение. Воспользуемся основным логарифмическим тождеством.

Тогда первое условие мы можем записать так: .

В условии у нас логарифм .

Перейдём ко второму условию .

Воспользуемся основным логарифмическим тождеством.

Тогда второе условие можно записать так: .

В условии у нас .

Подставим значение логарифма. Тогда имеем, .