Получите свидетельство
Вход
Известные вам способы решения алгебраических уравнений (подстановка, сложение, введение новых переменных) применяются и к решению систем, содержащих показательную функцию. Давайте рассмотрим решение систем показательных уравнений и неравенств на примерах.
Задание 1. Решите систему уравнений.
Решение.
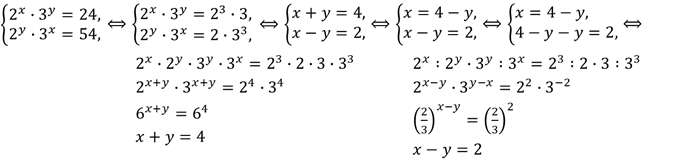
Ответ:
решением исходной системы уравнений является упорядоченная пара чисел 
.
Задание 2. Решите систему уравнений.
Решение.
Не
забудем записать ответ: решением нашей исходной системы являются упорядоченные
пары чисел 
.
Задание 3. Решите систему уравнений.
Решение.
Запишем
ответ: решением исходной системы уравнений является упорядоченная пара чисел 
.
Задание 4. Решите систему неравенств.
Решение.
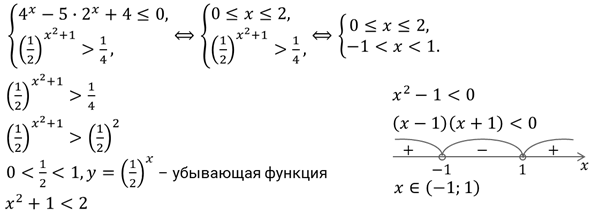
Ответ:
решением исходной системы неравенств является промежуток 
Задание 5. Решите систему неравенств.
Решение.
Ответ:
решением исходной системы неравенств является объединение
.
0
13450
