Группировка данных и гистограммы

Ребята, как известно, в статистике наборы данных представляют собой обширные массивы. Как правило, в массивах статистических данных совпадающие значения встречаются крайне редко (даже учитывая те случаи, когда данных очень много). Чаще встречаются близкие значения, которые разумно не различать.

Чтобы понять, насколько плотно распределены значения на каждом участке числовой прямой, применяют группировку данных.

Группировка данных – это показатель, который отражает плотность распределения значений в группах, разделённых по тем или иным признакам.

Чтобы сгруппировать данные, нужно разбить числовую прямую на одинаковые промежутки – интервалы группировки. Длина интервала называется шагом группировки. Потом нужно подсчитать долю значений в каждом интервале … Получаются частоты значений в интервалах. Затем остаётся построить диаграмму по полученным данным.

Отметим, что шаг группировки нужно выбирать так, чтобы, с одной стороны, диаграмма была достаточно подробной, а с другой – отражала тенденцию и хорошо показывала характер случайной изменчивости данных.

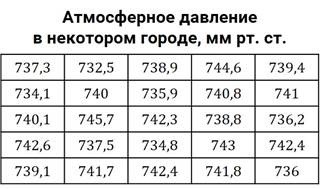
Давайте рассмотрим пример. Дана таблица, в которой приведены результаты измерений атмосферного давления в некотором городе в течение 25 дней. То есть всего у нас есть 25 значений.

Узнать, сколько всего значений в массиве данных, можно с помощью электронной таблицы, используя функцию СЧЁТ().

Наименьшее значение – 732,5 мм рт. ст. Наибольшее значение – 745,7 мм рт. ст. Пусть шаг группировки равен 3 мм рт. ст.

Для наглядности первый и последний интервалы сделаем пустыми, то есть в них не попадёт ни одно значение.

Отметим, что если значение попадает на границу двух интервалов, то его можно отнести к любому из них. Это вопрос договорённости. Давайте в этом примере мы будем относить граничное значение к левому интервалу.

Пусть первым будет интервал от 728 до 731. В него не попадает ни одно значение, то есть он пустой.

Вторым будет интервал от 731 до 734. В этот интервал попадает 1 значение.

Следующим будет интервал от 734 до737. В него попадает 5 значений.

Далее идёт интервал от 737 до 740. В этом интервале 7 значений. При этом обратите внимание, что сюда мы включили значение 740, так как договорились, что будем относить граничное значение к левому интервалу.

Затем идёт интервал от 740 до 743. В нём 10 значений.

Следующим будет интервал от 743 до 746. В этом интервале только 2 значения.

Интервал от 746 до 749, как мы и договаривались, будет пустым.

Получилось 7 интервалов.

Обратите внимание, что самым «населённым» является пятый интервал.

Теперь нам надо заполнить последний столбец таблицы. Для этого мы будем находить частоты попадания значений в интервал.

Итак, всего дано 25 значений. В первый интервал не попадает ни одно значение, а значит, частота равна 0.

Во второй интервал попадает 1 значение. Тогда получается, что частота равна 0,04.

В третий интервал попадает 5 значений. Следовательно, частота равна 0,2.

В следующий интервал попадает 7 значений. А значит, частота равна 0,28.

Так как в пятый интервал попадает 10 значений, то частота равна 0,4.

В шестой интервал попадает 2 значения. Следовательно, частота равна 0,08.

В последний интервал не попадает ни одно значение, а значит, частота равна 0.

Отметим, что для частот попадания в интервал верно то же свойство, которое было сформулировано и доказано для отдельных значений: сумма частот равна 1.

Чтобы отобразить полученную информацию наглядно, нужно построить гистограмму.

Гистограммой называется диаграмма частот. Гистограмма позволяет наглядно представить характер изменчивости данных.

Часто по внешнему виду гистограммы можно оценить среднее значение, медиану и выделить область концентрации значений.

Построим гистограмму по имеющимся данным.

Видим, что больше всего дней, когда атмосферное давление было в пределах от 740 мм рт. ст. до 743 мм рт. ст. Дней, когда давление было ниже 734 мм рт. ст. или выше 743 мм рт. ст., мало (сумма частот в соответствующих интервалах невелика).

Друзья, несмотря на то, что изначальных данных немного, общая закономерность прослеживается: очень малые и очень большие значения (то есть далёкие от центра) редки.

Давайте рассмотрим ещё один пример. В городской школе выбрали наугад 100 учеников и попросили замерить, сколько минут каждый из них тратит на дорогу в школу.

Давайте посмотрим на результаты.

Видим, что одинаковые значения встречаются редко, а число различных вариантов довольно велико.

Наибольшее значение – 55 мин. Наименьшее значение – 7 мин. Возьмём шаг группировки равный 8 мин.

Напомним, что если значение попадает на границу двух интервалов, то его можно отнести к любому из них. Давайте в этом примере мы будем относить граничное значение к правому интервалу.

Пусть первым будет интервал от 3 до 11. В него попадает 6 значений.

Вторым будет интервал от 11 до 19. В этот интервал попадает 8 значений.

Следующим будет интервал от 19 до 27. В него попадает 17 значений.

Далее идёт интервал от 27 до 35. В этом интервале 24 значения.

Затем идёт интервал от 35 до 43. В нём 23 значения.

Следующим будет интервал от 43 до 51. В этом интервале 13 значений.

Последний интервал (от 51 до 59ти) содержит 9 значений

Получилось 7 интервалов.

Обратите внимание, что самыми «населёнными» являются четвёртый и пятый интервалы.

Давайте заполним последний столбец таблицы. Для этого будем находить частоты попадания значений в интервал.

Итак, всего дано 100 значений. В первый интервал попадает 6 значений. А значит, частота равна 0,06.

Во второй интервал попадает 8 значений. Тогда получается, что частота равна 0,08.

В третий интервал попадает 17 значений. Следовательно, частота равна 0,17.

В четвёртый интервал попадает 24 значения. А значит, частота равна 0,24.

В следующий интервал попадает 23 значения. Тогда получается, что частота равна 0,23.

Так как в шестой интервал попадает 13 значений, то частота равна 0,13.

В последний интервал попадает 9 значений, а значит, частота равна 0,09.

Теперь запишем сумму найденных частот. Выполним сложение и получим 1.

Чтобы отобразить полученную информацию наглядно, построим гистограмму.

Видим, что в среднем школьники тратят на дорого около получаса. А это достаточно много времени.

В завершение нашего занятия отметим, что в электронной таблице искать количество значений, попавших в каждый интервал группировки, легко, если научиться пользоваться функцией ЧАСТОТА().

Но будьте внимательны! Функция ЧАСТОТА находит не частоту, а количество значений в интервалах.

До встречи на следующих занятиях!