Видеоучебник / Физика / Решение задач по физике. Механика 7-11 класс. / Движение тел по наклонной плоскости

Движение тел по наклонной плоскости

Урок 15. Решение задач по физике. Механика 7-11 класс.

Сложность решения задач по этой теме в первую очередь связана с тем, что многие ученики не способны правильно выбрать наилучшую систему координат и определить проекции векторов действующих сил на выбранные оси. В предложенном видеоуроке подробно, шаг за шагом разбираются решения задач по данной теме с рассмотрением правил построения проекций всех сил, действующих на исследуемое тело.

Конспект урока "Движение тел по наклонной плоскости"

«Требуются очень глубокие знания,

чтобы заметить простейшие, но

подлинные отношения вещей между собой».

Георг Кристоф Лихтенберг

Данная тема будет посвящена изучению движения тел по наклонной плоскости.

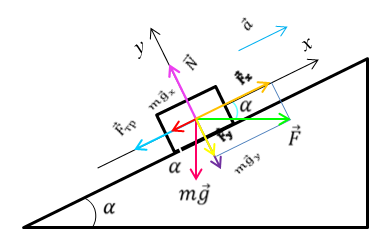
Задача 1. Тело массой 20 кг перемещается вверх по наклонной плоскости с углом наклона 45^о и коэффициентом трения 0,03. Определите ускорение, с которым движется тело, если к нему параллельно основанию плоскости приложена сила 650 Н.

ДАНО:

РЕШЕНИЕ:

На основании второго закона Ньютона, составим уравнение движения тела

В проекциях на ось Оx:

В проекциях на ось Оy:

Тогда сила трения равна

Следовательно

Преобразуем последнюю формулу

Тогда ускорение, с которым движется тело равно

Ответ: 14,8 м/с².

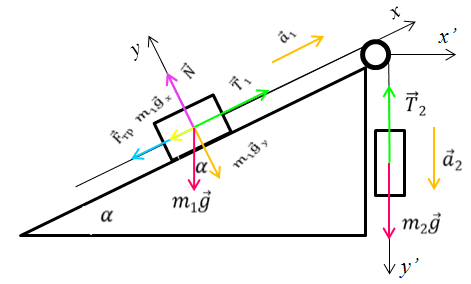
Задача 2. Тело массой 4 кг перемещается вверх по наклонной плоскости под действием связанного с ним невесомой и нерастяжимой нитью грузом массой 12 кг. Начальные скорости тела и груза равны нулю, коэффициент трения тела о плоскость равен 0,05, угол наклона плоскости равен 30^о. Определите ускорение, с которым движется тело, и силу натяжения нити. Считать, что блок невесом и трение в блоке отсутствует.

ДАНО:

РЕШЕНИЕ:

Запишем второй закон Ньютона для тела и груза

В проекциях на ось Ох:

В проекциях на ось Оy:

В проекциях на ось О’y’:

Получаем систему уравнений

Так как нить невесома и нерастяжима, а в блоке отсутствует трение, то:

С учётом последних выражений преобразуем систему уравнений

Для того, чтобы решить эту систему уравнений сложим первое и второе уравнение. Тогда получим

Преобразуем данное уравнение и выразим искомое ускорение

Теперь определим силу натяжения нити

Ответ: 6,4 м/с²; 43,2 Н.

Задача 3. Два груза массами т₁ = 5 кг и т₂ = 2 кг связаны невесомой нерастяжимой нитью, переброшенной через невесомый блок, который прикреплен к вершине призмы, и могут скользить по граням этой призмы. Определите ускорение грузов, если начальные скорости грузов равны нулю, α = 60^о, β = 30^о, а коэффициент трения — 0,3.