Получите свидетельство
Вход
«Мыслящий ум не чувствует себя счастливым,
пока ему не удастся связать воедино
разрозненные факты, им наблюдаемые»
Г.Ч. де Хевеши
В данной теме будут рассмотрены задачи на движение связанных тел.
Задача 1. Через блок перекинута невесомая и нерастяжимая нить, к концам которой подвешены два тела массами 1 и 2 кг. Тела предоставлены сами себе, а их начальные скорости равны нулю. Определите перемещение тел за 5 с движения, а также возникающую при этом силу в нити. Трением в блоке и его массой пренебречь.
|
ДАНО:
|
РЕШЕНИЕ:
Запишем второй закон Ньютона для первого и второго тела
В проекциях на ось Оу
Таким образом, получили систему из двух уравнений с четырьмя неизвестными. Для её решения необходимы еще два уравнения связи. Первое уравнение связи вытекает из условия о не растяжимости нити и отсутствия трения в блоке. Так как нить нерастяжима и в блоке нет трения, то:
Второе уравнение связи будет вытекать из условия о невесомости нити, которой наши тела связаны, и блока. Так как блок и веревка невесомы и нет трения в оси блока, то
Перепишем уравнения движения в следующем виде:
Для того чтобы решить полученную систему, вычтем из первого уравнения второе
Преобразуем уравнение
Кинематическое уравнение для правого тела:
В момент времени t = τ:
Тогда получаем
Теперь определим силу натяжения нити
|
Ответ: s = 41,7 м; T1 = T2 = 13,3 Н.
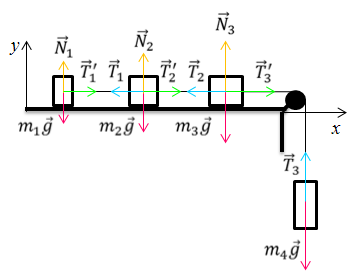
Задача 2. На гладкой горизонтальной поверхности находятся три бруска массами 1, 2 и 3 кг, связанные невесомыми нерастяжимыми нитями. К бруску большей массы на нити, перекинутой через неподвижный блок, подвешен груз массой 4 кг. Определите ускорение этой системы и силы натяжения всех нитей. Считать, что масса блока пренебрежимо мала и трение в блоке отсутствует.
|
ДАНО:
|
ДАНО:
Запишем второй закон Ньютона для всех четырёх связанных тел
Так как нить нерастяжима, то:
Так как нить невесома, то:
В проекциях на оси координат:
Для того, чтобы решить данную систему уравнений сложим три первых уравнения и вычтем четвёртое. Тогда получим
Теперь силы натяжения нитей
|
Ответ: a = 20 м/с2; Т1 = 20 Н; Т2 = 60 Н; Т3 = 120 Н.
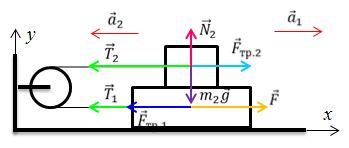
Задача 3. На гладком горизонтальном столе расположен брусок массой 5 кг, на котором находится брусок массой 3 кг. Оба бруска соединены легкой нерастяжимой нитью, перекинутой через невесомый блок. Если к нижнему бруску приложена сила 55 Н, а коэффициент трения между брусками равен 0,3, то чему равно ускорение, с которым движется система брусков?
|
ДАНО:
|
РЕШЕНИЕ:
Запишем второй закон Ньютона для каждого тела
Так как нить нерастяжима и в блоке нет трения, то:
Так как нить и блок невесомы, то:
Согласно третьему закону Ньютона, модули сил трения, действующие на бруски, также должны быть равны
В проекциях на ось Ох:
Вычтем второе уравнение из первого. Тогда получим
Преобразуем последнее уравнение и выразим из него ускорение
Учтем, что сила трения определяется по выражению
В проекциях на ось Оу:
Тогда ускорение будет равно
|
Ответ: 4,6 м/с2.
1
10206
Здравствуйте. Во второй задаче неверный расчет ускорения. В четвертом урвнении не учтен знак "-" ускорения четвертого тела, согласно выбранной системе координат.