Закон всемирного тяготения. Первая космическая скорость

На прошлом уроке мы с вами вспоминали о том, что наша планета у своей поверхности сообщает всем телам одинаковое ускорение — ускорение свободного падения. Но, как отмечалось ранее, раз земной шар сообщает телу ускорение, то, согласно второму закону Ньютона, он действует на тело с некоторой силой. Силу, действующую на тело со стороны Земли и сообщающую телу ускорение свободного падения, мы с вами назвали силой тяжести.

Но только ли Земля обладает свойством притягивать к себе тела? Конечно же нет. Ещё в седьмом классе вы узнали о том, что все без исключения тела притягиваются друг к другу с определённой силой — силой всемирного тяготения. Первые предположения о существовании этой силы высказывались многими учёными, среди которых и древнегреческий философ Эпикур, и немецкий астроном Иоганн Кеплер, и французский математик Рене Декарт. Но до Ньютона никто не сумел ясно и математически доказать её существование. Примерно в 1666 году он, прогуливаясь в яблоневом саду своих родителей, заметил в дневном небе Луну. А потом на его глазах с ветки дерева упало яблоко. «Хмм... а ведь оно упало не просто так, а под действием гравитационного поля Земли. Да и Луна тоже не просто висит на небе, а обращается вокруг Земли». И тут его осенило: «А вдруг сила, которая заставляет падать яблоко на землю, и сила, удерживающая Луну возле Земли, — это одна и та же сила?»

Дальше его рассуждения были достаточно просты. Он уже знал, что сила притяжения убывает пропорционально квадрату расстояния. Следовательно, Луна, расстояние до которой примерно равно 60 земным радиусам, должна испытывать ускорение в 3600 раз меньше, чем ускорение свободного падения вблизи поверхности Земли. Зная, что ускорение свободного падения вблизи поверхности нашей планеты равно 9,8 м/с², то можно легко определить орбитальное ускорение Луны, которое сообщает ей Земля:

С другой стороны, Луна, как и любое движущееся по окружности тело, обладает центростремительным ускорением:

Период обращения Луны вокруг Земли равен 27,32 сут, а радиус Земли — 6400 км = 3,84 ∙ 10⁸ м. Тогда получается, что орбитальное ускорение Луны примерно равно тем же 0,0027 м/с².

Вывод очевиден: сила, удерживающая Луну на орбите, — это сила земного притяжения, только ослабленная в 3600 раз, по сравнению с действующей у поверхности Земли.

А так как сила тяготения сообщает всем телам одинаковое ускорение независимо от их массы, то она должна быть пропорциональна массе того тела, на которое действует (в нашем случае Луны). Однако тогда по третьему закону Ньютона Луна должна действовать на Землю с точно такой же силой, но пропорциональной уже́ массе Земли.

Можно только догадываться о волнении, которое охватило великого учёного, когда он пришёл к такому великому результату: «Тяготение существует ко всем телам вообще и пропорционально массе каждого из них... Все планеты тяготеют друг к другу...»

Так был сформулирован закон всемирного тяготения: любые два тела притягивают друг друга силами, прямо пропорциональными произведению масс этих тел и обратно пропорциональными квадрату расстояния между ними:

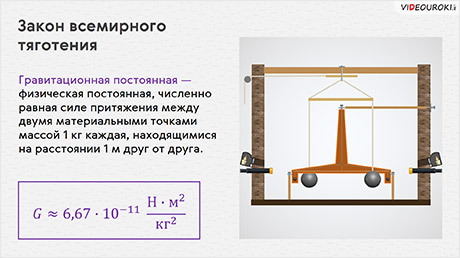
Коэффициент пропорциональности G, входящий в формулу, получил название гравитационной постоянной. Она численно равна силе притяжения между двумя материальными точками массой один килограмм каждая, находящимися на расстоянии одного метра друг от друга. Единицей её измерения в СИ является ньютон, умноженный на квадратный метр и делённый на килограмм в квадрате:

Что касается числового значения гравитационной постоянной, то оно может быть найдено только опытным путём. Но здесь возникает трудность: если массы взаимодействующих тел и расстояние между ними определить легко, то вот с силой возникают проблемы. Дело в том, что гравитационные силы, действующие между небольшими телами, очень малы́. Например, два среднестатистических человека (т = 73 кг), находящиеся на расстоянии одного метра друг от друга, притягиваются с силой всего лишь порядка миллионной доли ньютона. Поэтому для измерения гравитационной постоянной нужны были достаточно тонкие опыты.

Первые такие эксперименты были проведены Генри Кавендишем спустя примерно 132 года после открытия закона всемирного тяготения. Он поставил перед собой задачу проверить универсальность гравитационного взаимодействия. Для этого он использовал усовершенствованные крутильные весы, сконструированные Джоном Мичеллом.

Они представляли собой длинное коромысло с двумя небольшими свинцовыми шарами на концах, массы и диаметры которых заранее известны. Коромысло подвешивалось на тонкой упругой металлической нити. К малым шарам с помощью поворотного механизма подводились два больших тяжёлых свинцовых шара. Сила притяжения между двумя парами шаров заставляла небольшие шары перемещаться к большим. Это вызывало закручивание подвеса, угол которого определялся с помощью луча света, отражённого от зеркальца. По углу закручивания подвеса можно было определить силу, действующую между большими и малыми шарами.

Позднее по результатам эксперимента Кавендиша было получено значение гравитационной постоянной, отличающейся всего лишь на 1 % от ныне принятого значения.

Таким образом, Ньютон показал, что причиной, вызывающей падение камня на Землю, движение Луны вокруг Земли и планет вокруг Солнца, является сила всемирного тяготения. Кроме того, он предположил, что если бы не сопротивление воздуха, то траектория камня, брошенного с очень высокой горы с определённой скоростью, могла бы стать такой, что он вообще никогда не достиг бы поверхности Земли, а двигался бы под действием силы тяготения вокруг неё на постоянном расстоянии (подобно тому, как планеты описывают в небесном пространстве свои орбиты). Проще говоря, камень станет искусственным спутником Земли.

Под искусственными спутниками мы будем понимать космические аппараты, созданные людьми, которые позволяют наблюдать за планетой, вокруг которой они вращаются, а также за другими астрономическими объектами из космоса.

Интересно, что искусственным спутником Земли может стать любое тело произвольной массы. Важно, чтобы ему сообщили за пределами земной атмосферы горизонтальную скорость, при которой оно начнёт двигаться по окружности вокруг Земли.

Скорость, при достижении которой космический аппарат, запускаемый с Земли, может стать её искусственным спутником, называется первой космической скоростью.

Давайте подсчитаем её значение. Итак, пусть наш спутник находится за пределами земной атмосферы. Следовательно, силы сопротивления его движению практически отсутствуют и на него действует только сила притяжения к планете. Поэтому спутник движется как свободно падающее тело с ускорением свободного падения.

Кроме этого, сила всемирного тяготения сообщает спутнику центростремительное ускорение. Выберем ось координат так, чтобы её положительное направление совпало с направлением действия силы, и запишем уравнение движения спутника в проекциях на эту ось:

Силу, входящую в уравнение движения, мы определим из закона всемирного тяготения:

Обратите внимание на то, что знаменатель в формуле представляет собой расстояние от центра Земли до спутника. Центростремительное же ускорение спутника мы найдём как отношение квадрата его линейной скорости к радиусу орбиты:

Перепишем второй закон Ньютона с учётом последних двух формул:

Из полученного равенства, выполнив простые математические преобразования, получим формулу для определения первой космической скорости на любой высоте над поверхностью Земли:

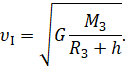
Обратите внимание на то, что эта скорость не зависит от массы спутника, но зависит от его расстояния от поверхности Земли: чем оно больше, тем меньше скорость спутника на круговой орбите.

Если можно пренебречь высотой спутника в сравнении с радиусом Земли, то первая космическая скорость может быть рассчитана по формуле, которую вы видите на экране:

Все величины, входящие в формулу, — это известные константы. И если подставить их значения, то получится, что для Земли первая космическая скорость примерно равна 7,91 км/с.

Именно такую скорость в горизонтальном направлении нужно сообщить телу на небольшой, сравнительно с радиусом Земли, высоте, чтобы оно не упало на Землю, а стало её спутником, движущимся по круговой орбите.

Запуск первого в мире искусственного спутника Земли состоялся 4 октября 1957 года с пятого научно-исследовательского полигона Министерства обороны СССР «Тюра-Там» (будущего космодрома «Байконур»). Он получил кодовой обозначение «ПС-1» («Простейший Спутник-1»).

Сейчас в околоземном пространстве движутся многие тысячи искусственных спутников Земли, запущенные учёными разных стран мира. Но возникает закономерный вопрос: раз спутники движутся как свободно падающие тела, то почему они не падают на поверхность Земли, а непрерывно вращаются вокруг неё?

Ответ достаточно прост. Примем для упрощения вычислений, что ускорение свободного падения равно 10 м/с², а первая космическая скорость — 8 км/с. Тогда получается, что за одну секунду движения спутник пройдёт по направлению к Земле всего 5 м. В то время, как перпендикулярно этому направлению он переместится на 8 км. В результате сложения этих двух движений спутник и движется по своей орбите.

В заключение отметим, что закон всемирного тяготения является одним из фундаментальных законов природы. Но не стоит забыть, что он был сформулирован для материальных точек. Однако, как показали расчёты, он достаточно точно выполняется и для однородных тел шарообразной формы, даже если их нельзя принять за материальные точки. А также при взаимодействии сферического тела произвольного размера с телом произвольной формы небольших размеров, находящимся вблизи поверхности сферы.

Для астрономических объектов закон всемирного тяготения выполняется всегда. Но для тел, находящихся сравнительно близко друг к другу (например, Земля и Луна или Плутон и Харон), точные измерения обнаруживают небольшие отклонения. В первую очередь это связано с их неоднородным и несферическим распределением масс.