Периодичность функций y=sinx, y=cosx

Вопросы занятия:

·     познакомиться с понятием периодичности;

·     познакомиться с понятием основного периода;

·     узнать основные периоды функций y=sin x, y=cos x.

Материал урока.

Прежде чем приступить к изучению нового материала, давайте повторим основные свойства функций y = sin x, y = cos x.

Давайте с вами посмотрим на рисунки.

Что мы там видим? Правильно, одно и тоже дерево, но в разные поры года. А на этом рисунке мы видим рушник с геометрическим орнаментом, а здесь – бьющееся сердце. А еще у нас есть приливы и отливы. Что объединяет все эти рисунки? А объединяет их то, что в каждом из приведенных примером есть повторяющиеся элементы. Так, когда мы смотрим на дерево в разные поры года, то мы знаем, что каждая пора повторяется через девять месяцев. Орнамент состоит из повторяющихся элементов. А биение сердца можно описать как повторяющиеся, через определённое время ритмы, сокращения сердечной мышцы. Приливы и отливы также возникают через одинаковое время.

Все эти примеры являются наглядными примерами периодичности.

Определение.

Периодичность – это повторяемость (цикличность) явления через определённые промежутки времени.

А теперь давайте вспомним, как мы вводили понятие синуса и косинуса. Эти понятия мы вводили, используя числовую окружность. Мы говорили, что на числовой окружности можно отложить бесконечно точек. Нами было доказано следующее утверждение.

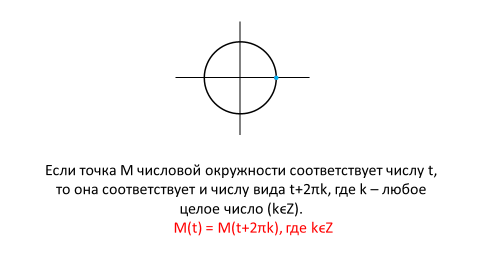
Какую же функцию мы будем называть периодической?

Определение.

Функцию y = f(x), где x принадлежит множеству X называют периодической, если существует такое отличное от нуля число T, что для любого x из множества X выполняется двойное равенство:

f(x-T) = f(x) = f(x+t)

Число T, удовлетворяющее указанному условию, называют периодом функции y = f(x).

Мы знаем, что для любого x справедливы равенства:

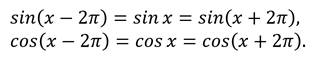
Значит, мы можем сказать, что функции y=sin x, y=cos x – периодические функции, с периодом 2π.

Давайте теперь посмотрим на графики наших функций.

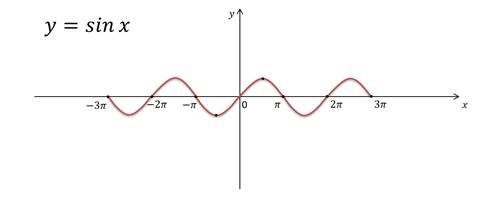
Легко заметить, что для того, чтобы построить график функции, достаточно построить одну волну синусоиды и затем сдвинуть эту волну по оси Ox на 2π влево и на 2π вправо, на 4π и на 4π вправо и так далее. Получается, что, построив одну волну, мы легко построим и весь график. Аналогично и для графика функции y = cos x.

Обобщая, можно сделать следующие выводы.

Рассмотрим пример.

Пример.

Рассмотрим ещё один пример.

Пример.

Заметим, что свойством периодичности обладают все тригонометрические функции.

Рассмотрим ещё один пример.

Пример.