Наибольшее и наименьшее значения функции

Сегодня на уроке мы вспомним, что называют наибольшим и наименьшим значениями функции. Научимся находить наибольшее и наименьшее значения функции на отрезке.

Прежде чем приступить к рассмотрению новой темы, давайте вспомним, что, говоря о наибольшем или наименьшем значении функции, её рассматривают на всей области определения или на числовом промежутке (отрезке, интервале и так далее), который является подмножеством области определения.

Пусть функция 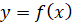 определена на числовом множестве .

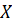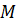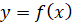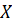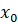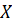Число  называется наибольшим значением функции  на числовом множестве , если существует  из  такое, что 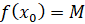, и для любого  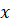из 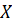 большое выполняется неравенство .

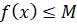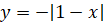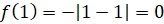Например, функция . Её область определения – множество действительных чисел. Число 0 – наибольшее значение функции на всей области определения, так как  и 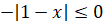 при любом значении  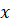из области определения функции. В этом случае можно записать:  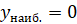при .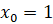

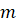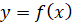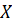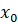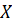Число  маленькое называется наименьшим значением функции  на числовом множестве , если существует  из  такое, что 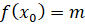, и для любого  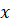из 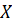 выполняется неравенство .

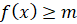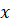Например, функция . Её область определения – множество действительных чисел. Число  – наименьшее значение функции на всей области определения, так как  и , то есть  при любом значении  из области определения функции.  В этом случае можно записать:  при .

На практике часто приходится решать задачи, в которых требуется найти наибольшее или наименьшее значение из всех значений, которые функция принимает на отрезке.

Посмотрите на график функции , который построен на отрезке .

Видим, что наибольшее значение на этом отрезке, равное 0, функция принимает в точке  и в точке . Наименьшее значение, равное , функция принимает при .

Точка  является точкой минимума данной функции. Это означает, что есть такая окрестность точки , например, интервал , что в этой окрестности функция принимает своё наименьшее значение при .

Но на отрезке  функция принимает наименьшее значение не в точке минимума, а на конце отрезка. Таким образом, для нахождения наименьшего значения функции на отрезке нужно сравнить её значения в точках минимума и на концах отрезка.

Итак, пусть функция  непрерывна на отрезке  и имеет несколько критических точек на этом отрезке. Для нахождения наибольшего и наименьшего значений функции на отрезке  нужно:

1) найти значения функции на концах отрезка, то есть числа  и ;

2) найти её значения в тех критических точках, которые принадлежат интервалу ;

3) из всех найденных значений найти наибольшее и наименьшее.

Рассмотрим пример. Функция  непрерывна на отрезке . Найдите её наибольшее и наименьшее значения.

Отметим, что наибольшее и наименьшее значения функции часто приходится находить не на отрезке, а на интервале. Встречаются задачи, в которых функция  имеет на заданном интервале одну стационарную точку: точку минимума или точку максимума. В этих случаях в точке максимума функция  принимает наибольшее значение на данном интервале, а в точке минимума – наименьшее значение на данном интервале.

Давайте решим задачу. Число  представьте в виде суммы двух положительных слагаемых так, чтобы сумма квадратов этих чисел была наименьшей.

А сейчас сформулируем утверждение, которое полезно использовать при решении некоторых задач на нахождение наибольшего и наименьшего значений функции.

Если значения функции  неотрицательны на некотором промежутке, то эта функция и функция , где  – натуральное число, принимают наибольшее (наименьшее) значение в одной и той же точке.

А сейчас выполним задание.

Найдите наибольшее и наименьшее значения функций на заданных отрезках:

а) , ; б) , .

Решение.