Применение производной к построению графиков функций

Сегодня на уроке мы приведём общую схему исследования свойств функции с помощью её производной. Будем строить график функции, используя результаты исследования.

Прежде чем приступить к рассмотрению новой темы, давайте вспомним, что на предыдущих занятиях мы рассмотрели применение производной к нахождению промежутков возрастания и убывания функций. Выяснили, какие точки называют точками максимума функции и точками минимума функции. Научились находить эти точки и значения функции в них. Сегодня на уроке мы применим эти знания к построению графиков функций.

Давайте начнём с примера. Итак, постройте график функции .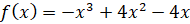

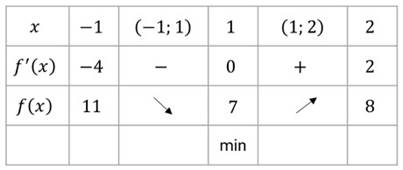
Полученные результаты исследования функции удобно записать в виде следующей таблице.

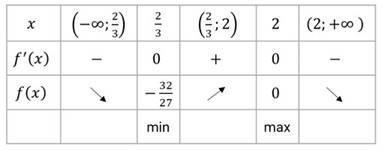
В первой строке этой таблицы указаны в порядке возрастания критические точки функции и ограниченные ими промежутки. Во второй строке отмечены знаки производной на этих промежутках. В третьей строке записаны выводы о ходе изменения данной функции, в четвёртой строке – о виде критических точек.

При построении графика обычно находят точки пересечения графика с осями координат.

Построим график функции.

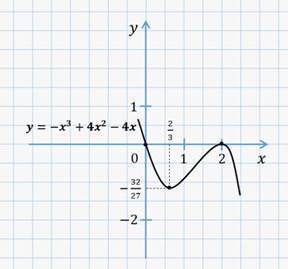
Получается, что для построения графика функции сначала исследуют свойства этой функции с помощью её производной.

Давайте приведём схему исследования свойств функции с помощью её производной.

Итак, при исследовании свойств функции надо найти:

1) область определения; производную; стационарные точки;

2) промежутки возрастания и убывания;

3) точки экстремума и значения функции в этих точках.

Результаты исследования удобно записать в виде таблицы, используя которую, строят график функции. Для более точного построения графика обычно находят точки пересечения с осями координат. Также можно найти координаты ещё нескольких точек графика.

Отметим, что для построения графика чётной (нечётной) функции достаточно исследовать свойства и построить её график при 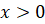, а затем отразить его симметрично относительно оси ординат (начала координат).

Давайте построим график функции .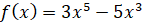

Полученные результаты исследования запишем в виде таблицы.

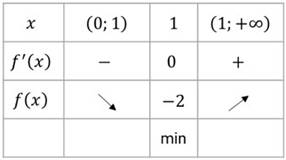
Найдём значение функции в точке 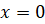 – крайней точке рассматриваемого интервала. .

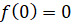Построим график функции.

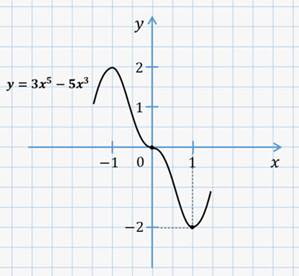
Так как рассматриваемая функция является нечётной, то её график при 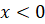 строим с помощью симметрии относительно начала координат.

Часто встречаются задачи, в которых требуется исследовать функцию не на всей области определения, а на некотором промежутке.

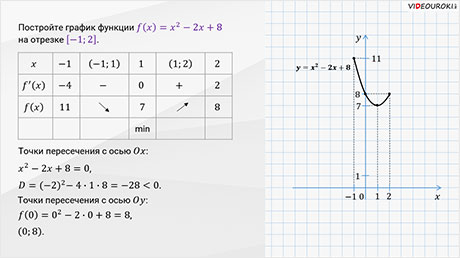
Давайте построим график функции 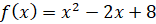 на отрезке .

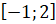Запишем полученные результаты исследования функции в виде таблицы.

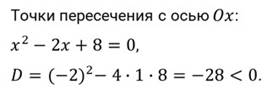
Получается, что график функции не пересекает ось абсцисс.

Построим график функции.