Представим себе такую историю…
– Саша, чем ты занимаешься? – спросил у друга Паша.
– Решаю анаграммы, – ответил Саша. – Смотри, как много я решил. А вот на этой застрял… – загрустил Саша.

– Давай попробуем вместе, – предложил Паша. – Здесь написано, что так называют числа, произведение которых равно единице. Что-то не припомню я таких чисел, – задумался Паша. – Ну, не беда. Попробуем сложить из этих букв слова. Смотри: из букв первого слова можно составить слово «взаимно».
– Точно! – обрадовался Саша. – А из последнего – слово «числа».
– Осталось расшифровать второе слово, – продолжил Паша.
– Я попробую, – загорелся Саша. – Батон… Бетон… Набор… Тенор… – стал перечислять он. – Но что-то всё не то получается!
– Мне кажется, я понял, – сказал Паша. – Это слово «обратные».
– Точно! – обрадовался Саша. – Тогда получается, что здесь зашифрована фраза «взаимно обратные числа»? – удивился он. – Что это за числа такие?
– В условии у тебя написано, что так называют числа, произведение которых равно единице, – сказал Паша.
– И какие же это числа надо так умножить, чтобы получить единицу? – недоумевал Саша.
– Не знаю, – задумался Паша, – но точно знаю, кто нам сможет объяснить.

– Ребята, прежде чем я расскажу вам о взаимно обратных числах, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.

– Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было получиться!
–
Ну а теперь вернёмся к вашему вопросу, – начал Мудряш. – Давайте рассмотрим
дробь  .
Если её «перевернуть», то есть поменять местами числитель и знаменатель, то
получим дробь
.
Если её «перевернуть», то есть поменять местами числитель и знаменатель, то
получим дробь  .
Полученную дробь называют обратной к дроби
.
Полученную дробь называют обратной к дроби  .
Понятно, что если из данных двух дробей первая обратна ко второй, то вторая
обратна к первой. То есть и дробь
.
Понятно, что если из данных двух дробей первая обратна ко второй, то вторая
обратна к первой. То есть и дробь  обратна
к дроби
обратна
к дроби  .
Поэтому про такие дроби можно говорить, что это дроби, обратные друг к
другу.
.
Поэтому про такие дроби можно говорить, что это дроби, обратные друг к
другу.
– Может, вы сможете привести примеры обратных друг к другу дробей? – спросил у ребят Мудряш.
–
Дроби  и
и
 ,
,
 и
и
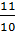 ,
– начал Саша.
,
– начал Саша.
–
Дроби  и
и
 ,
,
 и
и
 ,
– продолжил Паша.
,
– продолжил Паша.
– Молодцы! – похвалил ребят Мудряш. – А теперь давайте попробуем перемножить наши обратные друг к другу дроби и посмотрим, что же получится.
–
 умножим
на
умножим
на  ,
– начал Паша. – Запишем произведение числителей и знаменателей этих дробей.
Сократим числитель и знаменатель на 3, затем на 5. Получим дробь
,
– начал Паша. – Запишем произведение числителей и знаменателей этих дробей.
Сократим числитель и знаменатель на 3, затем на 5. Получим дробь  ,
или 1.
,
или 1.
–
Перейдём к следующей паре дробей  и
и
 ,
– продолжил Саша. – Запишем произведение числителей и знаменателей этих дробей.
Сократим сначала на 4, потом – на 7. Тоже получим дробь
,
– продолжил Саша. – Запишем произведение числителей и знаменателей этих дробей.
Сократим сначала на 4, потом – на 7. Тоже получим дробь  ,
или 1.
,
или 1.
–
Найдём произведение дробей  и
и
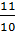 ,
– сказал Паша. – Запишем произведение числителей и знаменателей. Сократим
числитель и знаменатель на 10, затем на 11. Снова получим дробь
,
– сказал Паша. – Запишем произведение числителей и знаменателей. Сократим
числитель и знаменатель на 10, затем на 11. Снова получим дробь  ,
или 1.
,
или 1.
–
Перейдём к следующему произведению  и
и
 ,
– сказал Саша. — Запишем произведение числителей и знаменателей этих дробей.
Сократим сначала на 4, потом на 5. И опять получим дробь
,
– сказал Саша. — Запишем произведение числителей и знаменателей этих дробей.
Сократим сначала на 4, потом на 5. И опять получим дробь  ,
или 1.
,
или 1.
–
Осталось вычислить произведение дробей  и
и
 ,
– сказал Паша. –
,
– сказал Паша. –  —
это же просто 100. Значит, умножим дробь
—
это же просто 100. Значит, умножим дробь  на
100. Затем сократим. И снова получим дробь
на
100. Затем сократим. И снова получим дробь  ,
или 1.
,
или 1.
– Всё правильно посчитали, – сказал Мудряш. – Какой вывод можно сделать?
– Произведение дробей, обратных друг к другу, равно единице, – сказали мальчишки.

– Молодцы! – похвалил ребят Мудряш. – Запомните! Два числа, произведение которых равно единице, называют взаимно обратными.
– Получается, что обратные друг к другу дроби являются взаимно обратными числами? – решили уточнить мальчишки.
–
Верно, – ответил Мудряш. – Числа  и
и
 –
взаимно обратные, так как их произведение равно 1.
–
взаимно обратные, так как их произведение равно 1.  и
и
 —
тоже взаимно обратные числа.
—
тоже взаимно обратные числа.  и
и
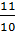 –
взаимно обратные числа.
–
взаимно обратные числа.  и
и
 –
взаимно обратные числа.
–
взаимно обратные числа.  и
и
 –
взаимно обратные числа.
–
взаимно обратные числа.
– А теперь проверьте, будут ли взаимно обратными числами следующие пары чисел, – предложил Мудряш.
–
 и
и
 –
взаимно обратные числа, – начал Паша. – Если мы запишем данные десятичные дроби
в виде обыкновенных, то убедимся, что их произведение
–
взаимно обратные числа, – начал Паша. – Если мы запишем данные десятичные дроби
в виде обыкновенных, то убедимся, что их произведение  .
.
–
Следующая пара чисел —  и
и
 ,
– продолжил Саша, – тоже взаимно обратные числа. Второе число смешанное, если
его записать в виде неправильной дроби, то увидим, что произведение
,
– продолжил Саша, – тоже взаимно обратные числа. Второе число смешанное, если
его записать в виде неправильной дроби, то увидим, что произведение  .
.
–
 и
и
 –
взаимно обратные числа, – сказал Паша. – Десятичную дробь
–
взаимно обратные числа, – сказал Паша. – Десятичную дробь  представим
в виде обыкновенной дроби
представим
в виде обыкновенной дроби 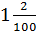 .
Можем сократить числитель и знаменатель дробной части на 2. Получим смешанное
число
.
Можем сократить числитель и знаменатель дробной части на 2. Получим смешанное
число  .
Затем запишем это число в виде неправильной дроби
.
Затем запишем это число в виде неправильной дроби  .
Найдём произведение дробей. Видим: произведение этих чисел также равно 1.
.
Найдём произведение дробей. Видим: произведение этих чисел также равно 1.

–
Всё верно! – согласился Мудряш. – Запомните! Числом, обратным
единице, является само число один. А вот для числа ноль обратного числа не
существует. Обратным числу  является
число
является
число  .
Действительно, ведь
.
Действительно, ведь  .
.
– А какое число будет обратно натуральному числу, например 5? – спросили ребята.
–
Поскольку любое натуральное число эн можно представить в виде дроби  ,
то можно сделать следующий вывод. Если
,
то можно сделать следующий вывод. Если 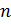 –
натуральное число, то обратным ему является число
–
натуральное число, то обратным ему является число  .
.
–
Это значит, что числу 5 обратным будет число  ?
– уточнили мальчишки.
?
– уточнили мальчишки.
– Правильно! – согласился Мудряш. – А теперь, ребята, давайте посмотрим, как вы всё поняли, и решим несколько заданий.
Задание
первое: найдите число, обратное к числу: а)  ;
б)
;
б)  ;
в)
;
в)  ;
г)
;
г)  .
.
Решение: запишем
число 0,5 в виде обыкновенной дроби  .
Сократим числитель и знаменатель этой дроби на 5. Получим дробь
.
Сократим числитель и знаменатель этой дроби на 5. Получим дробь  .
Тогда искомое число
.
Тогда искомое число  ,
или просто 2.
,
или просто 2.
1,7
равна смешанному числу 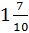 .
В свою очередь, смешанное число
.
В свою очередь, смешанное число 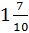 равна
неправильной дроби
равна
неправильной дроби  .
Тогда искомое число —
.
Тогда искомое число — 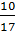 .
.
Следующее
число —  .
Искомым будет число
.
Искомым будет число 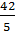 .
.
И
последнее число —  .
Запишем его в виде неправильной дроби
.
Запишем его в виде неправильной дроби  .
Тогда обратным числу
.
Тогда обратным числу  является
число
является
число  .
.

Следующее
задание: будут ли взаимно обратными числа: а)  и
и
 ;
б)
;
б)  и
и
 ;
в)
;
в)  и
и
 ;
г)
;
г)  и
и
 ?
?
Решение: чтобы ответить на вопрос, будут ли числа являться взаимно обратными, нужно убедиться, что их произведение равно 1. Первая пара чисел 0,4 и 2,5. Найдём их произведение. Оно равно 1. Следовательно, числа 0,4 и 2,5 – взаимно обратные.
Следующая пара чисел — 0,2 и 2. Сразу видим, что эти числа не будут являться взаимно обратными, так как их произведение не равно 1.
Перейдём
к следующей паре чисел. Смешанное число  запишем
в виде неправильной дроби
запишем
в виде неправильной дроби  .
Десятичную дробь 0,9 представим в виде обыкновенной дроби
.
Десятичную дробь 0,9 представим в виде обыкновенной дроби  .
Найдём произведение дробей. Получим дробь
.
Найдём произведение дробей. Получим дробь  .
Видим: произведение не равно 1, значит, числа
.
Видим: произведение не равно 1, значит, числа  и
0,9 не являются взаимно обратными числами.
и
0,9 не являются взаимно обратными числами.
И
рассмотрим последнюю пару чисел. Десятичную дробь 1,234 запишем смешанным
числом  .
Можем сократить дробную часть на 2. Получим смешанное число
.
Можем сократить дробную часть на 2. Получим смешанное число  .
Затем представим это число в виде неправильной дроби
.
Затем представим это число в виде неправильной дроби 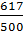 .
Найдём произведение дробей
.
Найдём произведение дробей 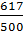 и
и
 .
Видим: произведение этих дробей равно 1, следовательно, числа 1,234 и
.
Видим: произведение этих дробей равно 1, следовательно, числа 1,234 и  являются
взаимно обратными числами.
являются
взаимно обратными числами.


 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 2286
2286