Деление дробей

Представим себе такую историю…

– Саша, о чём ты задумался? – спросил у друга Паша.

– Мама купила в магазине мои любимые конфеты, – начал Саша. – За  килограмма конфет она заплатила  рубля. Мне стало интересно, сколько же тогда стоит 1 килограмм моих любимых конфет.

– И что тут сложного? – удивился Паша. – Возьми и посчитай.

– Чтобы узнать, сколько стоит один килограмм конфет, – начал Саша, – нужно всю сумму, которую мама заплатила, разделить на массу купленных конфет. То есть нужно  разделить на . Но мы же ещё не знаем, как делят дроби.

– Ну да, – согласился Паша. – А давай поразмышляем вместе. Мы знаем, что действие деления обратно действию умножения, то есть делением находят неизвестный множитель по произведению и известному множителю. Значит, надо найти такое число, которое при умножении на  даст .

– Похоже, что да! – сказал Саша. – Но как-то всё равно пока не понятно.

– Давай попробуем переписать наши смешанные числа в виде неправильных дробей, – предложил Паша. – Так как произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей, то можем заметить, что в знаменателе нашего неизвестного числа будет стоять двойка.

– Тогда в числителе будет стоять … так, так, так… надо подумать, – начал размышлять Саша. – 161 разделим на 7. Получается 23. Значит, в числителе будет записано число 23. Следовательно, число которое мы искали, – .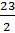

– То есть килограмм моих любимых конфет стоит 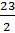 рубля? – недоумевал Саша. – И что, каждый раз надо так подбирать числа в числитель и знаменатель?

– Давай лучше спросим у Мудряша, – предложил Паша. – Раз есть правила сложения, вычитания и умножения дробей, значит, должно существовать и правило деления дробей.

– Ребята, прежде чем я расскажу вам о делении дробей, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.

– Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было получиться!

– Ну а теперь вернёмся к вашему вопросу, – начал Мудряш. – Заметим, что частное 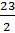 можно получить в результате умножения делимого  на дробь, обратную делителю , то есть на дробь . Действительно,  умножить на  равно 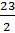. Тогда имеем, что  разделить на  равно  умножить на  и равно .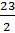

– Вообще, деление дробей можно свести к умножению дробей, пользуясь следующим правилом.

– Запомните! – сказал Мудряш. – Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю. В буквенном виде это правило записывают так: .

– А теперь давайте потренируемся и найдём частное следующих дробей, – предложил Мудряш.

– Найдём частное дробей  и , – начал Саша. – Применим правило деления дробей. Напомним, что два числа, произведение которых равно единице, называют взаимно обратными. Значит, числом, обратным делителю , будет дробь . Тогда деление дроби  на  можем заменить на произведение дробей  и . Воспользуемся правилом умножения дробей. Получим дробь .

– Перейдём к следующему частному, – сказал Паша. — Представим сначала числа  и  в виде неправильных дробей:  и . Применим правило деления дробей. Числом, обратным делителю , является дробь . Тогда деление дроби  на  можем заменить на произведение дробей  и . Затем воспользуемся правилом умножения дробей. Можем сократить числитель и знаменатель дроби сначала на 5, потом на 4. Получим дробь . Это неправильная дробь, так как числитель больше знаменателя. Значит, выделим целую часть. В результате получим .

– Следующее частное дроби  и 6, – продолжил Саша. – Применим правило деления дробей. Числом, обратным делителю 6, будет дробь , так как мы знаем, что если  – натуральное число, то обратным ему является число . Тогда деление дроби  на 6 можем заменить на произведение дробей  и . Затем воспользуемся правилом умножения дробей. Получим дробь .

– И найдём последнее частное, – сказал Паша. – Применим правило деления дробей. Число 5 представим дробью со знаменателем 1. Числом, обратным делителю, является дробь . Тогда деление дроби  на  можем заменить на произведение дробей  и . Затем воспользуемся правилом умножения дробей. Получим дробь . Это неправильная дробь, так как числитель больше знаменателя. Выделим целую часть. В результате получим число .

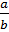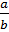– Также вам следует знать, – сказал Мудряш, – что если 1 разделить на дробь , то получим дробь . Если 0 разделить на дробь , то получим 0. И напомню, что на 0 делить нельзя.

А теперь, ребята, давайте посмотрим, как вы всё поняли, и решим несколько заданий.

Задание первое: решите уравнения: а) ;      б) ;       в) ;        г) .

Решение: первое уравнение . Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель. Применим правило деления дробей. Число  представим в виде неправильной дроби . Числом, обратным делителю, является . Тогда деление заменим на умножение. Получим, что . Сократим числитель и знаменатель дроби на 7, затем сократим на 4. Отсюда .

Следующее уравнение . Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель. Делитель 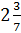 представим в виде неправильной дроби . Применим правило деления дробей. Получим, что .

Третье уравнение . Чтобы найти неизвестное слагаемое, нужно от суммы отнять известное слагаемое. Число  представим в виде неправильной дроби , число  представим в виде неправильной дроби . Теперь приведём все три наши дроби к наименьшему общему знаменателю 12. Дополнительный множитель к первой дроби равен 3, ко второй – 4, к третьей – 2. Применим правило вычитания дробей с одинаковыми знаменателями. Тогда . Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель. Применим правило деления дробей. Сократим числитель и знаменатель дроби на 12, затем на 3. Получим, что . Это неправильная дробь, выделим целую часть. Получим, что.

И последнее уравнение . Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить известное вычитаемое. Тогда . Или . Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель. Воспользуемся правилом деления дробей. Сократим числитель и знаменатель дроби на 4. Отсюда .

Следующее задание: площадь прямоугольника равна  м². Найдите периметр прямоугольника, если его ширина  метра.

Решение: мы знаем, что площадь прямоугольника равна произведению длин его соседних сторон. Тогда неизвестная сторона равна частному дробей  и . Применим правило деления дробей. Сократим числитель и знаменатель дроби на 3, затем на 8. Получаем, что вторая сторона равна  метра. Периметр прямоугольника равен удвоенной сумме длин соседних его сторон. Подставим в формулу значения сторон нашего прямоугольника. В скобках получим 1. Тогда периметр прямоугольника равен 2 метрам. Запишем ответ.