Для начала посмотрим, как получить изображения точечного источника света в собирающей и рассеивающей линзах. Для этого мы с вами в основном будем пользоваться тремя «удобными лучами», ход которых после прохождения через линзу нам заранее известен:
Во-первых, это луч, идущий параллельно главной оптической оси, так как после преломления в линзе, он проходит через её главный фокус (или проходит его продолжение).

Из закона обратимости световых лучей следует, что луч, который идёт к линзе через её фокус, после преломления будет направлен параллельно главной оптической оси — это второй «удобный» луч.
И третий луч выбираем исходя из того, что луч, проходящие через оптический центр линзы, не меняет своего направления.
Точка пересечения преломлённых лучей в собирающей линзе или их продолжений в рассеивающей, и даёт нам положение изображения точечного источника света.
Усложним задачу. Пусть точечный источник света располагается на главной оптической оси линзы. Чтобы найти, где образуется изображение, проведём от источника света два луча.

Первый луч пустим вдоль главной оптической оси линзы, который, проходя через оптический центр, не испытывает преломления. А второй луч направим под некоторым углом к линзе. Теперь проведём побочную оптическую ось, проходящую через оптический центр линзы параллельно падающему лучу. Далее проведём заднюю фокальную плоскость для собирающей линзы, или переднюю для рассеивающей. Побочная оптическая ось пересечёт фокальную плоскость в побочном фокусе. Через этот побочный фокус и пойдут все параллельные данной оптической оси лучи после преломления в собирающей линзе, или продолжения преломлённых лучей в рассеивающей линзе.
Преломлённый луч (или его продолжение) пересечёт главную оптическую ось в точке, которая и будет являться изображением точечного источника света.
При этом изображение в собирающей линзе будет являться действительным, так как оно получилось на пересечении самих преломлённых лучей, а в рассеивающей — мнимым, так как оно получено на пересечении продолжений преломлённых лучей.
Теперь проведём небольшой опыт. На столе расположим экран, собирающую линзу и зажжённую свечу, удалённую от линзы на расстояние, большее, чем удвоенное фокусное расстояние линзы. Будем передвигать экран в направлении к линзе до тех пор, пока на экране не увидим чёткое изображение пламени свечи. Что мы можем сказать об этом изображении?

Во-первых, оно уменьшенное. Во-вторых, — перевёрнутое. Но самое главное в том, что это изображение реально существует, так как на экране концентрируется энергия света. Если поместить чувствительный термометр в изображение пламени свечи, то он покажет небольшое повышение температуры.
Подтвердим сказанное построением. Итак, для получения изображения точки А воспользуемся двумя лучами. Первый луч пустим вдоль главной оптической оси линзы. Так как он проходит через оптический центр, то он не испытывает преломления, поэтому мы его просто продолжаем за линзу.
Второй луч направим под некоторым углом к линзе. Проводим побочную оптическую ось, проходящую через центр линзы параллельно падающему лучу. И указываем положение задней фокальной плоскости. Точка пересечения побочной оптической оси́ и фокальной плоскости даёт нам положение побочного фокуса, через который пойдут все параллельные данной оптической оси лучи после преломления в линзе. Преломлённый луч пересечёт главную оптическую ось в точке, которая и будет являться изображением точки «А» предмета.
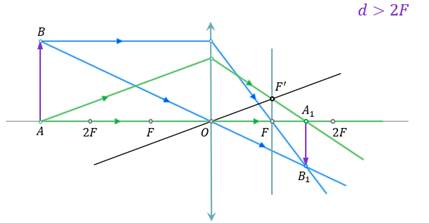
Чтобы построить изображение точки В, направим луч света параллельно главной оптической оси линзы. После преломления, этот луч, как мы уже знаем, пойдёт через главный фокус линзы. Второй луч можно направить через оптический центр линзы. В точке пересечения этих двух лучей и будет находиться изображение нашей точки В. Соединяя точки А1 и В1 получим изображение предмета АВ в линзе.
Полученное нами изображение предмета является действительным, так как оно получилось на пересечении преломлённых лучей. Во-вторых, оно перевёрнутое. И, как можно видеть из построения, оно уменьшенное.
Обратите внимание, что если предмет расположен перпендикулярно главной оптической оси, то и его изображение также будет перпендикулярно ей. Зная это, мы сможем построить изображение точки В просто опустив перпендикуляр из точки А1 на главную оптическую ось, что мы и будем делать в дальнейшем.
Продолжим опыт. Поставим свечу на расстоянии, равному двойному фокусному. Перемещая экран, мы со временем увидим на нём действительное, перевёрнутое изображение пламени свечи, размер которого будет равен размеру пламени самой свечи. Сделайте сами построение изображения для этого случая.
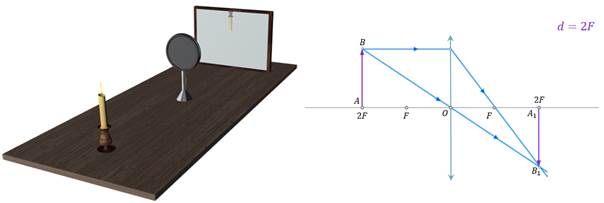
Как видим, и вправду оно у нас получилось действительным, перевёрнутым и равным по высоте предмету.
Передвинем свечу так, чтобы она находилась между первым и вторым фокусом линзы (F < d < 2F). После небольших манипуляций с экраном мы сможем увидеть на нём действительное, перевёрнутое, увеличенное изображение пламени свечи. Докажем и этот случай построением.
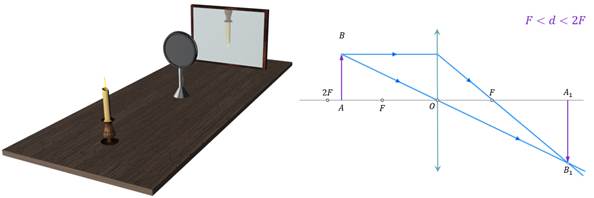
Теперь передвинем нашу свечу так, чтобы она находилась в главном фокусе линзы. Как бы мы теперь ни перемещали экран, изображения пламени свечи мы не увидим — изображения нет. И действительно, если мы построим ход лучей для этого случая, то увидим, что преломлённые линзой лучи не пересекаются, как и не пересекаются их продолжения. Следовательно, изображения в этом случае действительно отсутствует.
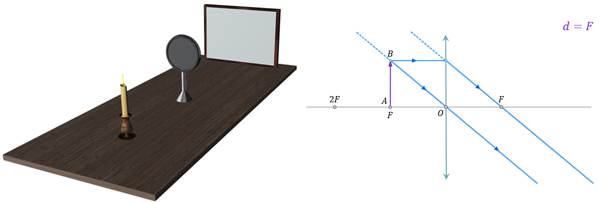
И, наконец, поставим свечу между главным фокусом и линзой. Изображения свечи и в этом случае не видно. Давайте построим ход лучей в линзе для этого случая.
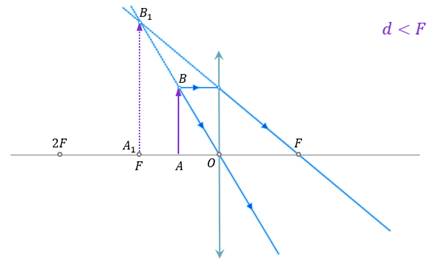
Как видим, преломлённые лучи расходятся. Но вот их продолжения пересекаются. Поэтому изображение предмета будет мнимым, увеличенным, прямым и находиться со стороны изображаемого предмета. Именно так и работает увеличительное стекло, используемое людьми для рассмотрения мелких объектов.
При построении изображения предметов в рассеивающей линзе поступают точно так же, как и в случае с собирающей. Единственное отличие состоит в том, что у рассеивающей линзы фокус мнимый.
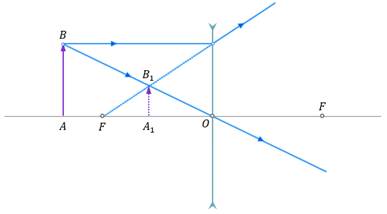
Поэтому изображение, даваемое рассеивающей линзой, всегда мнимое, прямое, уменьшенное и находится между линзой и её фокусом со стороны изображаемого предмета.
Теперь давайте выведем формулу, которая свяжет три величины — расстояние от предмета до линзы, расстояние от линзы до изображения и фокус линзы. Все размышления, которые мы будем проводить для собирающей линзы, справедливы и для линзы рассеивающей.
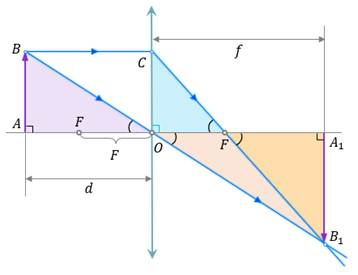
Итак, рассмотрим два треугольника: ΔАОВ и ΔА1ОВ1. Эти треугольники подобны по стороне и прилежащим к ней углам. Следовательно, можно записать, что:

Аналогично, из подобия треугольников ΔОCF и ΔА1В1F находим, что:

Также из построений видно, что AB = OC. А A1F = A1O – OF. Исходя из этого, мы можем записать, что:

Заменим стороны треугольников через введённые нами ранее обозначения.

Теперь преобразуем полученное уравнение, воспользовавшись известными математическими приёмами:

Разделив полученное равенство на множитель Ffd, и преобразовав выражение так, как это показано на экране, получим формулу тонкой линзы для нашего случая:

В общем же виде формула тонкой линзы записывается следующим образом: сумма величин, обратных расстояниям от предмета до линзы и от линзы до изображения, равна величине, обратной фокусному расстоянию:

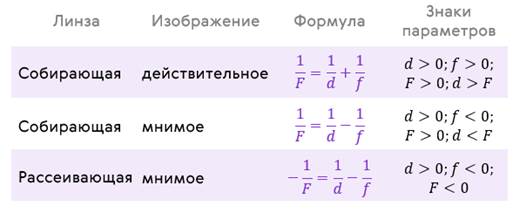
Для практического использования формулы тонкой линзы не забываем про правило знаков:
· для собирающей линзы, действительных источника и изображения, фокусное расстояние, расстояние от предмета до линзы и от линзы до изображения считают положительными;
· для рассеивающей линзы, мнимых источника и изображения, фокусное расстояние, расстояние от предмета до линзы и от линзы до изображения считают отрицательными.
Как вы могли заметить, чаще всего, изображение, получаемое с помощью тонкой линзы, отличается своими размерами от предмета. Так вот, это различие между размерами предмета и размерами его изображения принято характеризовать линейным (или поперечным) увеличением линзы.
Если обозначить размеры предмета буквой h, а размеры изображения — H, то линейное увеличение линзы равно отношению линейного размера изображения к линейному размеру предмета:

Если вернуться к нашему рисунку для вывода формулы тонкой линзы, то из подобия треугольников ΔAOB и ΔA1OB1 следует, что:

Тогда можно записать, что линейное увеличение линзы равно отношению расстояния от линзы до изображения к расстоянию от предмета до линзы:


 Получите свидетельство
Получите свидетельство Вход
Вход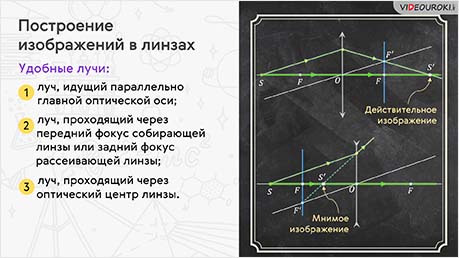




 1078
1078

