Определение:
Окружность - это геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.

Точка О - центром окружности, а отрезок ОМ, соединяющий центр с точкой М, лежащей на окружности, называется радиусом окружности. Радиус окружности обычно обозначают буквой r. Из определения окружности следует, что все радиусы имеют равную длину.
Возьмём некоторую окружность с центром в точке О. Отметим на этой окружности две произвольные точки А и В и соединим их.

Полученный отрезок АВ называется хордой окружности. А вот хорда СD, проходящая через центр окружности, называется диаметром. Диаметр окружности в два раза больше её радиуса, то есть СD=ОD. Также отметим, что центр окружности является серединой любого диаметра. Любые две точки окружности делят её на две части, каждая из которых называется дугой окружности. CDB и CAB - дуги окружности, ограниченные точками С и В.
Для изображения окружности на чертеже используют циркуль. А вот на местности окружность можно провести с помощью верёвки.

Часть плоскости, ограниченная окружностью, называется кругом.

Ранее вы уже проводили прямые и откладывали отрезки, чертили углы, треугольники и другие геометрические фигуры.

При этом вы использовали такие инструменты как масштабная линейка, транспортир, циркуль, чертёжный угольник.

В геометрии выделяют задачи на построение, которые можно решить, используя только циркуль и линейку без масштабных делений.
С помощью линейки можно:
· провести произвольную прямую;
· построить прямую, проходящую через две данные точки.
С помощью циркуля можно:
· провести окружность произвольного радиуса;
· провести окружность с центром в данной точке и радиусом, равным данному отрезку.
Пример.
На данном луче от его начала отложить отрезок, равный данному.
Изобразим луч ОС и отрезок АВ.

Построим окружность радиуса АВ с центром в точке О.

Полученная окружность пересекает луч ОС в некоторой точке D. Отрезок OD и является искомым.
Пример.
Отложить от данного луча угол, равный данному.
Возьмём некоторый угол с вершиной в точке А и некоторый луч ОМ.

Нам нужно построить угол, равный углу А, так, чтобы одна из его сторон совпала с лучом ОМ. Проведём окружность произвольного радиуса с центром в точке А.

Окружность пересекает стороны угла в точках В и С.
Проведём окружность такого же радиуса с центром в точке О. Она пересекает луч в точке D.

Затем построим окружность с центром в точке D, радиус которой равен ВС.

Окружности с центрами О и D пересекаются в двух точках.

Докажем, что ∠МОЕ - искомый угол. Рассмотрим ∆ АВС и ∆ ODE.

Отрезки АВ и АС - радиусы окружности с центром в точке А. OD и OE - радиусы окружности с центром в точке О. По построению данные окружности имеют равные радиусы, поэтому АВ=OD и АС=ОЕ. А также по построению ВС=DE.
Следовательно, треугольники АВС и ODE равны по третьему признаку равенства треугольников. Поэтому ∠ВАС=∠DОЕ, то есть построенный ∠MOE равен углу с вершиной в точке А.
Пример.
Даны прямая а и точка М, лежащая на данной прямой. Построить прямую, проходящую через данную точку и перпендикулярную этой прямой.

На лучах прямой а, исходящих из точки М, отложим равные отрезки МА и МВ. Построим окружность с центром в точке А радиуса АВ и окружность с центром в точке В радиуса АВ.

Полученные окружности пересекаются в точках P и Q. Проведя прямую МР, докажем, что эта прямая искомая. Для этого рассмотрим треугольник АРВ, который является равнобедренным, так как РА и РВ - равные радиусы окружностей с центром в точках А и В соответственно.

РМ является медианой треугольника, проведённой к основанию. А значит, является и высотой, то есть прямая РМ перпендикулярна прямой а.
Следует отметить, что не существует единого алгоритма решения задач на построение. Каждая задача требует индивидуального подхода для решения.

 Получите свидетельство
Получите свидетельство Вход
Вход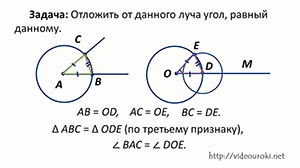



 0
0 9626
9626