На этом уроке мы вспомним понятие цилиндра. Дадим его определение. Рассмотрим, какими элементами обладает цилиндр.
Вокруг нас существует множество объектов, которые являются физическими моделями цилиндра, или проще говоря, имеют форму цилиндра.
Например, кружки и стаканы имеют форму цилиндра. Карандаши, шляпы, пуфики, барабан также имеют форму цилиндра.

Некоторые архитектурные сооружения.

Колонны храмов и соборов, выполненные в форме цилиндра, подчеркивают их гармонию и красоту.
Итак, перейдём к самому цилиндру. Рассмотрим
произвольную плоскость ![]() и окружность
и окружность ![]() с центром О
радиуса
с центром О
радиуса ![]() , лежащую в этой
плоскости. Через каждую точку окружности
, лежащую в этой
плоскости. Через каждую точку окружности ![]() проведем прямую,
перпендикулярную к плоскости
проведем прямую,
перпендикулярную к плоскости ![]() .
.
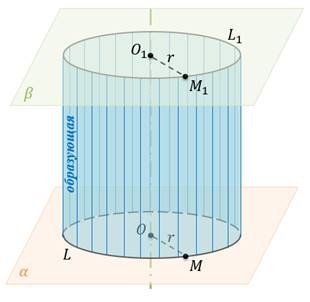
Определение:
Поверхность, образованная этими прямыми, называется цилиндрической поверхностью, а сами прямые – образующими цилиндрической поверхности.
Прямая, проходящая через точку О перпендикулярно к
плоскости ![]() , называется осью
цилиндрической поверхности. Поскольку все образующие и ось
перпендикулярны к плоскости
, называется осью
цилиндрической поверхности. Поскольку все образующие и ось
перпендикулярны к плоскости ![]() , то они
параллельны друг другу.
, то они
параллельны друг другу.
Рассмотрим теперь плоскость ![]() , параллельную
плоскости
, параллельную
плоскости ![]() . Отрезки
образующих, заключённые между плоскостями
. Отрезки
образующих, заключённые между плоскостями ![]() и
и ![]() , параллельны и
равны друг другу. По построению концы этих отрезков, расположенные в плоскости
, параллельны и
равны друг другу. По построению концы этих отрезков, расположенные в плоскости ![]() , заполняют
окружность
, заполняют
окружность ![]() . Концы же,
расположенные в плоскости
. Концы же,
расположенные в плоскости ![]() , заполняют
окружность
, заполняют
окружность ![]() с центром
с центром ![]() радиуса
радиуса ![]() , где
, где ![]() – точка
пересечения плоскости
– точка
пересечения плоскости ![]() с осью
цилиндрической поверхности. Справедливость этого утверждения следует из того,
что множество концов образующих, лежащих в плоскости
с осью
цилиндрической поверхности. Справедливость этого утверждения следует из того,
что множество концов образующих, лежащих в плоскости ![]() , получается из
окружности
, получается из
окружности ![]() параллельным
переносом на вектор
параллельным
переносом на вектор ![]() . Параллельный
перенос является движением и, значит, наложением, а при наложении любая фигура
переходит в равную ей фигуру. Следовательно, при параллельном переносе на
вектор
. Параллельный
перенос является движением и, значит, наложением, а при наложении любая фигура
переходит в равную ей фигуру. Следовательно, при параллельном переносе на
вектор ![]() . окружность
. окружность ![]() перейдёт в равную
ей окружность
перейдёт в равную
ей окружность ![]() радиуса
радиуса ![]() с центром в точке
с центром в точке
![]() .
.
Определение:
Тело, ограниченное цилиндрической поверхностью и двумя
равными кругами с границами ![]() и
и ![]() , называется цилиндром.
, называется цилиндром.
Можно ещё услышать и такое определение: прямым
круговым цилиндром или просто цилиндром называется
геометрическое тело, ограниченное цилиндрической поверхностью и двумя
параллельными плоскостями ![]() и
и ![]() , которые
перпендикулярны образующим цилиндрической поверхности.
, которые
перпендикулярны образующим цилиндрической поверхности.
Назовём элементы цилиндра.
Круги называются основаниями цилиндра.
Отрезки образующих, заключенные между основаниями, - образующими цилиндра.
А образованная ими часть цилиндрической поверхности это есть боковая поверхность цилиндра.
Ось цилиндрической поверхности называется осью цилиндра.
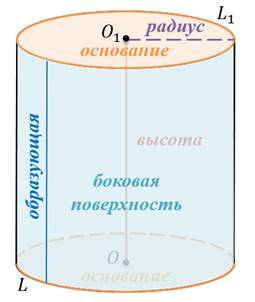
Как уже отмечалось ранее, все образующие цилиндра параллельны и равны друг другу. Длина образующей называется высотой цилиндра, а радиус основания – радиусом цилиндра.
Цилиндр называется равносторонним, если его высота равна диаметру основания.
Боковой поверхностью цилиндра называется часть цилиндрической поверхности, расположенная между основаниями цилиндра.
Цилиндр можно получить вращением прямоугольника вокруг
одной из его сторон на ![]() . Итак, если взять
некоторый прямоугольник
. Итак, если взять
некоторый прямоугольник ![]() и вращать его
вокруг одной из сторон, например, вокруг стороны
и вращать его
вокруг одной из сторон, например, вокруг стороны ![]() , то в результате
получим тело, которое и называется цилиндром.
, то в результате
получим тело, которое и называется цилиндром.
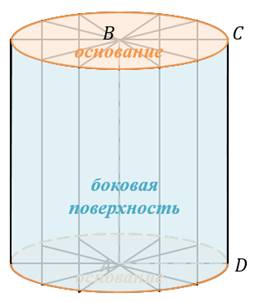
В этом случае основания цилиндра
образуются вращением сторон ![]() и
и ![]() , а боковая
поверхность цилиндра образуется вращении стороны
, а боковая
поверхность цилиндра образуется вращении стороны ![]() .
.
Теперь рассмотрим сечения цилиндра различными плоскостями.
Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра. Такое сечение называется осевым.
Определение:
Осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через его ось.
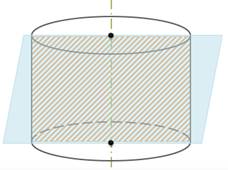
Если секущая плоскость параллельна оси цилиндра, то сечением цилиндра служит прямоугольник, две стороны которого – образующие цилиндра, а две другие – хорды оснований цилиндра.
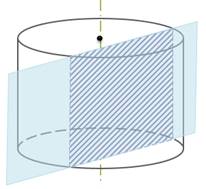
Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом.
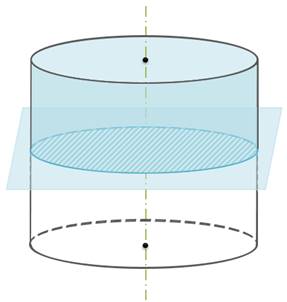
В самом деле, такая секущая плоскость отсекает от данного цилиндра тело, которое также является цилиндром. Его основаниями служат два круга, один из которых и есть рассматриваемое сечение.
Замечание. На практике очень часто встречаются предметы, которые имеют форму сложных цилиндров.
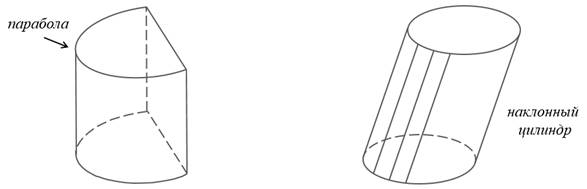
На экране, на первом рисунке вы видите цилиндр, каждое основание которого представляет собой фигуру, ограниченную частью параболы и отрезком. На втором рисунке изображен цилиндр, основаниями которого являются круги, но образующие цилиндра не перпендикулярны к плоскостям оснований, такой цилиндр называют еще наклонным цилиндром. Однако в дальнейшем мы будем рассматривать только прямые круговые цилиндры.
Задача: точка
![]() – середина образующей
– середина образующей ![]() цилиндра,
центрами оснований которого являются точки
цилиндра,
центрами оснований которого являются точки ![]() и
и ![]() . Верно ли, что
. Верно ли, что ![]() ?
?
Решение: рассмотрим
![]() и
и ![]() .
.

Образующая ![]() перпендикулярна
плоскостям, в которых лежат основания цилиндра. Следовательно, она
перпендикулярна любой прямой лежащей в этих плоскостях. Прямые
перпендикулярна
плоскостям, в которых лежат основания цилиндра. Следовательно, она
перпендикулярна любой прямой лежащей в этих плоскостях. Прямые ![]() и
и ![]() являются
радиусами цилиндра и лежат в плоскостях оснований. Значит, прямая
являются
радиусами цилиндра и лежат в плоскостях оснований. Значит, прямая ![]() и
и ![]() . Отсюда получаем,
что
. Отсюда получаем,
что ![]() и
и ![]() – прямоугольные.
– прямоугольные.
Так как основаниями цилиндра являются равные круги, то
![]() , как радиусы.
, как радиусы.
Так как по условию задачи точка ![]() – середина
образующей
– середина
образующей ![]() цилиндра, то
отрезки
цилиндра, то
отрезки ![]() . Значит,
. Значит, ![]() равны по двум катетам.
Отсюда вытекает, что
равны по двум катетам.
Отсюда вытекает, что ![]() .
.
Ответ: ![]() .
.
Задача: точка
![]() – центр основания
цилиндра. Отрезок
– центр основания
цилиндра. Отрезок ![]() – диаметр другого
его основания. Вычислите площадь
– диаметр другого
его основания. Вычислите площадь ![]() , если радиус
цилиндра равен
, если радиус
цилиндра равен ![]() см, а его высота
–
см, а его высота
– ![]() см.
см.
Решение: напомним,
что площадь треугольника находится по формуле ![]() . Заметим, что
высота цилиндра является и высотой нашего
. Заметим, что
высота цилиндра является и высотой нашего ![]() и равна
и равна ![]() . А основание
треугольника есть диаметр цилиндра и равно оно двум радиусам, т.е.
. А основание
треугольника есть диаметр цилиндра и равно оно двум радиусам, т.е. ![]() (см).
(см).
Подставим в формулу площади треугольника высоту и
длину основания треугольника. Посчитаем. Получим, что площадь треугольника
равна ![]() . Не забудем
записать ответ.
. Не забудем
записать ответ.
Задача: радиус
цилиндра ![]() см, а его высота
–
см, а его высота
– ![]() см. Вычислите
площадь осевого сечения.
см. Вычислите
площадь осевого сечения.
Решение: напомним, что осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через его ось. Осевое сечение цилиндра представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра.
Высота цилиндра – это есть длина образующей ![]() . Следовательно,
ширина осевого сечения равна
. Следовательно,
ширина осевого сечения равна ![]() . Длина сечения
равна диаметру основания цилиндра. И значит, равна
. Длина сечения
равна диаметру основания цилиндра. И значит, равна ![]() (см).
(см).
Теперь вычислим площадь осевого сечения. Она равна ![]() (
(![]() ).
).
Запишем ответ.
Итоги:
На этом уроке мы вспомнили понятие цилиндра. Узнали,
что тело, ограниченное цилиндрической поверхностью и двумя кругами с границами ![]() и
и ![]() , называется
цилиндром. Или прямым круговым цилиндром или просто цилиндром называется
геометрическое тело, ограниченное цилиндрической поверхностью и двумя
параллельными плоскостями
, называется
цилиндром. Или прямым круговым цилиндром или просто цилиндром называется
геометрическое тело, ограниченное цилиндрической поверхностью и двумя
параллельными плоскостями ![]() и
и ![]() , которые
перпендикулярны образующим цилиндрической поверхности. Назвали элементы
цилиндра. А также рассмотрели сечения цилиндра различными плоскостями.
, которые
перпендикулярны образующим цилиндрической поверхности. Назвали элементы
цилиндра. А также рассмотрели сечения цилиндра различными плоскостями.

 Получите свидетельство
Получите свидетельство Вход
Вход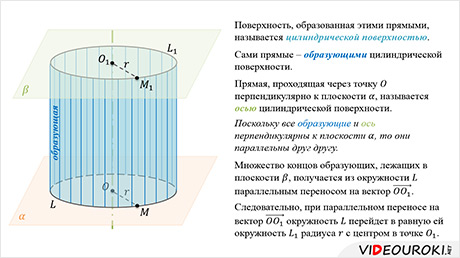



 0
0 9381
9381

