На этом уроке мы выведем и научимся применять формулы для вычисления площади боковой поверхности цилиндра и площади полной поверхности цилиндра.
Для начала давайте вспомним, что же это за
геометрическое тело – цилиндр. Итак, тело,
ограниченное цилиндрической поверхностью и двумя равными кругами с границами  и
и  , называется цилиндром.
, называется цилиндром.
Напомним, что боковой поверхностью цилиндра называется часть цилиндрической поверхности, расположенная между основаниями цилиндра.

На экране изображён цилиндр с радиусом  и высотой
и высотой
 . Давайте
представим себе, что его боковую поверхность разрезали по образующей
. Давайте
представим себе, что его боковую поверхность разрезали по образующей  и
развернули таким образом, что все образующие оказались расположенными в
некоторой плоскости
и
развернули таким образом, что все образующие оказались расположенными в
некоторой плоскости  .
.

В результате в плоскости  получится прямоугольник
получится прямоугольник  . Стороны
. Стороны  и
и  , которого
являются двумя краями разреза боковой поверхности цилиндра по образующей
, которого
являются двумя краями разреза боковой поверхности цилиндра по образующей  . Этот
прямоугольник называется развёрткой боковой поверхности цилиндра.
. Этот
прямоугольник называется развёрткой боковой поверхности цилиндра.
Обратите внимание, основание  прямоугольника является развёрткой окружности основания
цилиндра, отсюда сторона
прямоугольника является развёрткой окружности основания
цилиндра, отсюда сторона  равна длине окружности основания, т.е. равна
равна длине окружности основания, т.е. равна  , где
, где  – радиус
цилиндра. А сторона
– радиус
цилиндра. А сторона  равна
высоте цилиндра, т.е.
равна
высоте цилиндра, т.е.  .
.
Площадь боковой поверхности цилиндра равна
площади её развёртки. А так как развертка боковой поверхности цилиндра есть
прямоугольник  , то
площадь боковой поверхности цилиндра равна произведению длин сторон
прямоугольника
, то
площадь боковой поверхности цилиндра равна произведению длин сторон
прямоугольника  на
на  , или
равна
, или
равна  .
.

Итак, мы с вами вывели формулу для вычисления
площади боковой поверхности цилиндра радиуса  и высоты
и высоты  :
:  .
.
Получили, что площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту цилиндра.
Теперь выведем формулу для вычисления площади полной поверхности цилиндра.
Вообще, площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований.
Напомним, что основаниями цилиндра
являются два равных круга, каждый с площадью  . А
формулу для вычисления площади боковой поверхности цилиндра
. А
формулу для вычисления площади боковой поверхности цилиндра  мы с вами уже вывели выше. Подставим все данные в формулу.
Упростим.
мы с вами уже вывели выше. Подставим все данные в формулу.
Упростим.

Отсюда, получаем, что площадь полной
поверхности цилиндра можно вычислить по формуле:  .
.
А сейчас давайте решим несколько задач на применение выведенных формул.
Задача: цилиндр получен в
результате вращения прямоугольника  около
прямой
около
прямой  .
Вычислите площадь боковой поверхности цилиндра, если длины сторон
.
Вычислите площадь боковой поверхности цилиндра, если длины сторон  и
и  прямоугольника
равны соответственно
прямоугольника
равны соответственно  см и
см и  см.
см.
Решение: запишем формулу для вычисления площади боковой поверхности цилиндра.

Теперь внимательно рассмотрим рисунок.

Обратите внимание, сторона  прямоугольника
прямоугольника
 является
радиусом основания цилиндра. А сторона
является
радиусом основания цилиндра. А сторона  – это
высота нашего цилиндра.
– это
высота нашего цилиндра.

 см
см
Подставим эти данные в формулу для вычисления
площади боковой поверхности цилиндра. Посчитаем. Получим, что площадь боковой
поверхности нашего цилиндра равна  .
.
Запишем ответ.
Задача: осевое сечение цилиндра
– квадрат, длина диагонали которого равна  см.
Вычислите площадь боковой поверхности цилиндра.
см.
Вычислите площадь боковой поверхности цилиндра.
Решение: запишем формулу для вычисления площади боковой поверхности цилиндра.

Теперь рассмотрим рисунок.

Напомним, что осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через его ось. Осевое сечение представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра.
Так как по
условию задачи осевое сечение цилиндра квадрат  – квадрат , то
все стороны осевого сечения равны
– квадрат , то
все стороны осевого сечения равны  . Тогда получаем, что диаметр цилиндра равен высоте
цилиндра
. Тогда получаем, что диаметр цилиндра равен высоте
цилиндра  . А, значит, имеем равносторонний цилиндр.
. А, значит, имеем равносторонний цилиндр.
Найдём, чему
равна сторона осевого сечения. По условию нам дана длина диагонали квадрата. Значит,
можем вычислить и его сторону. Напомним, что диагональ квадрата можно вычислить
по формуле:  , где а сторона квадрата. Отсюда выразим
сторону квадрата. Тогда получим, что сторона осевого сечения равна
, где а сторона квадрата. Отсюда выразим
сторону квадрата. Тогда получим, что сторона осевого сечения равна 
 .
.
Так как радиус
равен половине диаметра, то 
 .
.
Подставим найденные
радиус основания цилиндра и его высоту в формулу для вычисления площади боковой
поверхности цилиндра. Посчитаем. Получим, что площадь боковой поверхности
цилиндра равна 
 .
.
Не забудем записать ответ.
Задача: высота цилиндра равна  см. Площадь сечения цилиндра плоскостью, параллельной
оси цилиндра и находящейся на расстоянии
см. Площадь сечения цилиндра плоскостью, параллельной
оси цилиндра и находящейся на расстоянии  см от нее, равна
см от нее, равна  см2. Вычислите площадь полной поверхности
цилиндра.
см2. Вычислите площадь полной поверхности
цилиндра.
Решение: запишем формулу для вычисления площади полной поверхности цилиндра.

Теперь рассмотрим рисунок.

Напомним, что если
секущая плоскость параллельна оси цилиндра, то сечением цилиндра служит
прямоугольник, две стороны которого – образующие цилиндра, а две другие – хорды
оснований цилиндра. Следовательно, сечением нашего цилиндра служит прямоугольник
 .
.
Ранее мы с вами
говорили, что высота цилиндра и его образующие параллельны и равны. Значит, стороны
 и
и  сечения равны
сечения равны  (см).
(см).
Найдём, чему
равны стороны  и
и  сечения. Так как площадь сечения равна 160 см2,
то стороны
сечения. Так как площадь сечения равна 160 см2,
то стороны  .
.
Рассмотрим  . Он равнобедренный, так его стороны
. Он равнобедренный, так его стороны  .
.
Так как
расстояние от точки до прямой – это есть перпендикуляр, то отрезок  является перпендикуляром, проведённым к стороне
является перпендикуляром, проведённым к стороне  . Следовательно,
. Следовательно,  – высота равнобедренного
– высота равнобедренного  , а, значит, и медиана по свойствам высоты
равнобедренного треугольника, проведенной к основанию.
, а, значит, и медиана по свойствам высоты
равнобедренного треугольника, проведенной к основанию.
Теперь
рассмотрим  . Он прямоугольный.
. Он прямоугольный. 
 .
.

 по условию.
по условию.
Отсюда, применяя
теорему Пифагора имеем, 
 .
.
Подставим
значения радиуса и высоты цилиндра в формулу для вычисления площади полной
поверхности цилиндра. Посчитаем. Получим, что площадь полной поверхности нашего
цилиндра равна  .
.
Запишем ответ.
Итоги:
На этом уроке мы вывели формулы для вычисления площади боковой поверхности цилиндра и площади полной поверхности цилиндра. А также научились их применять при решении задач.

 Получите свидетельство
Получите свидетельство Вход
Вход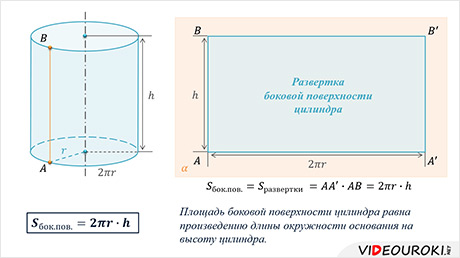



 0
0 7752
7752