Друзья, сегодня наше занятие будет посвящено уравнениям. Но прежде чем приступить к их решению, давайте проверим, насколько вы внимательны.
Найдите ошибки в приведённых примерах. Чем быстрее вы справитесь с этим заданием, тем лучше.

Ну а теперь посмотрите, какие из данных примеров оказались неверными.

Действительно, сумма 34 и 29 равна 63, а не 73.
50 плюс 75 минус 25 равно 100, а не 110.
Сумма 36 и 15, умноженная на 2, равна не 104, а 102.
90 разделить на 3 плюс 560 равно 590, а не 600.
А сейчас перед вами палитра. Но, как вы видите, там, где должны быть краски, записаны уравнения. Рядом с палитрой расположены разноцветные кружочки с ответами к данным уравнениям.

Чтобы наша палитра стала цветной, нам нужно решить уравнения. Каждому цвету соответствует число, которое можно получить в ответе.
Прежде чем приступить к решению, давайте вспомним, что уравнение – это равенство, содержащее букву, значение которой надо найти.
Корнем уравнения называется число, которое при подстановке вместо буквы обращает уравнение в верное числовое равенство. Корень уравнения также называется решением уравнения.
Решить уравнение – значит найти все его корни или убедиться, что их нет.
Также вспомним, что если к обеим частям уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получится уравнение, имеющее те же корни, что и данное.
Если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получится уравнение, имеющее те же корни, что и данное.
Если обе части уравнения умножить (или разделить) на одно и то же отличное от нуля число, то получим уравнение, имеющее те же корни, что и данное.
Давайте вернёмся к нашей палитре.
Начнём с уравнения:  .
.
Перенесём 133 и 57 в правую часть уравнения, изменив знаки этих слагаемых на противоположные.

Выполним вычисления в правой части уравнения и получим, что  . Значит, раскрашиваем соответствующий кружочек в красный цвет.
. Значит, раскрашиваем соответствующий кружочек в красный цвет.
Решим вот это уравнение:  .
.
В первую очередь раскроем скобки в его левой части. Для этого воспользуемся распределительным свойством умножения.

Затем перенесём  в правую часть уравнения, изменив знак этого слагаемого на противоположный.
в правую часть уравнения, изменив знак этого слагаемого на противоположный.

Выполним вычитание в правой части.

Теперь, чтобы найти неизвестный множитель  ,
,  разделим на
разделим на  . Получим, что
. Получим, что  . Раскрашиваем кружочек в жёлтый цвет.
. Раскрашиваем кружочек в жёлтый цвет.
Следующее уравнение:  .
.
Сначала раскроем скобки в его правой части. Для этого воспользуемся распределительным свойством умножения.

Затем  перенесём в правую часть уравнения, а
перенесём в правую часть уравнения, а  – в левую часть. При этом не забудем изменить знаки этих
слагаемых на противоположные.
– в левую часть. При этом не забудем изменить знаки этих
слагаемых на противоположные.

Приведём подобные слагаемые в левой части уравнения и выполним
вычисления в правой. Получим, что  . Откуда
. Откуда  . Значит, раскрашиваем кружочек
в зелёный цвет.
. Значит, раскрашиваем кружочек
в зелёный цвет.
Решим такое уравнение:  .
.
Для этого воспользуемся правилом нахождения неизвестного делителя: чтобы найти неизвестный делитель, надо делимое разделить на частное.

Частное  и
и  равно
равно  : Перенесём
: Перенесём  в правую часть, изменив знак слагаемого на противоположный.
в правую часть, изменив знак слагаемого на противоположный.

Выполнив вычисления в правой части.

Откуда находим, что  . А значит, раскрашиваем соответствующий кружочек в синий цвет.
. А значит, раскрашиваем соответствующий кружочек в синий цвет.
Чтобы решить уравнение  , перенесём
, перенесём  в его правую часть, а
в его правую часть, а  – в левую, не забыв изменить знаки этих слагаемых на
противоположные.
– в левую, не забыв изменить знаки этих слагаемых на
противоположные.

Приведём подобные слагаемые в левой части уравнения, и выполним вычитание в правой части.

Теперь, чтобы найти  , надо
, надо  разделить на
разделить на  . Выполнив деление, получим, что
. Выполнив деление, получим, что  . Следовательно, соответствующий кружочек надо раскрасить в голубой
цвет.
. Следовательно, соответствующий кружочек надо раскрасить в голубой
цвет.
Перейдём к решению следующего уравнения:  .
.
В первую очередь, воспользовавшись распределительным свойством умножения, раскроем скобки в его левой и правой частях.

Затем перенесём  и
и  в правую часть уравнения, а
в правую часть уравнения, а  – в его левую часть. При этом не забудем изменить знаки слагаемых
на противоположные.
– в его левую часть. При этом не забудем изменить знаки слагаемых
на противоположные.

Приведём подобные слагаемые в левой части и выполним вычисления в
правой. В результате получим, что  . Значит, раскрашивает этот кружочек в оранжевый цвет.
. Значит, раскрашивает этот кружочек в оранжевый цвет.
Осталось решить ещё одно уравнение:  .
.
Итак, в первую очередь раскроем скобки в левой части уравнения, воспользовавшись распределительным свойством умножения.

Затем приведём подобные слагаемые.

Перенесём  в правую часть уравнения. При этом не
забудем изменить знак слагаемого на противоположный.
в правую часть уравнения. При этом не
забудем изменить знак слагаемого на противоположный.

Сейчас, чтобы найти  , разделим
, разделим  на
на  . Получим, что
. Получим, что  . А значит, раскрашиваем кружочек в розовый цвет.
. А значит, раскрашиваем кружочек в розовый цвет.

Отлично! Палитра стала цветной.
А теперь, прежде чем завершить наше занятие, давайте решим с помощью уравнений несколько текстовых задач.
Задача первая. В первом ящике было в 2 раза больше груш, чем во втором. Когда из первого переложили 5 кг во второй, груш в ящиках стало поровну. Сколько груш было в каждом ящике?
Решение.

Задача вторая. Периметр прямоугольника равен 28 см. Одна из его сторон на 4 см больше другой. Чему равна площадь этого прямоугольника?
Решение.

Задача третья. Отцу 30 лет, а сыну 6 лет. Через сколько лет отец будет в 4 раза старше сына?
Решение.

Задача четвёртая. Легковой автомобиль проезжает расстояние между двумя населёнными пунктами за 7 ч, а автобус – за 9 ч. Скорость автобуса меньше скорости легкового автомобиля на 20 км/ч. Чему равно расстояние между населёнными пунктами?
Решение.

Ребята, вы отлично справились и с палитрой уравнений, и с задачами. Вы просто молодцы! До встречи на наших занятиях!

 Получите свидетельство
Получите свидетельство Вход
Вход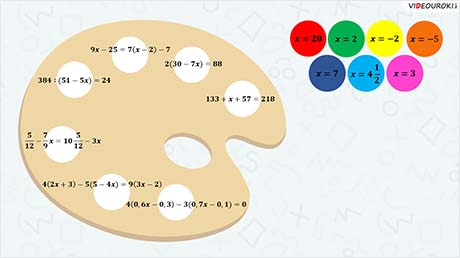




 550
550