Возрастание и убывание функции

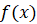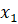Прежде чем приступить к рассмотрению новой темы, давайте вспомним, что функция  называется возрастающей на некотором промежутке, если большему значению аргумента соответствует большее значение функции, то есть для любых точек  и 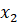 из этого промежутка, таких, что 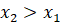, выполняется неравенство .

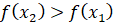Если для любых точек 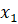 и 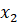 из данного промежутка, таких, что и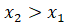, выполняется неравенство 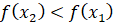, то функция  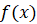называется убывающей на этом промежутке.

Нахождение промежутков возрастания и убывания функции – это одна из основных задач исследования функции. Такое исследование легко провести с помощью производной. Давайте рассмотрим применение производной к нахождению промежутков возрастания и убывания функций.

Итак, пусть дана функция 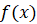. Значения производной этой функции положительны на некотором промежутке. Тогда угловой коэффициент касательной к графику этой функции положителен в каждой точке данного промежутка. А значит, касательная образует острый угол с осью 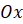. Поэтому можно сказать, что график функции «поднимается» на этом промежутке, то есть функция 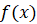 возрастает.

Если значения производной данной функции отрицательны на некотором промежутке, то угловой коэффициент касательной к графику функции 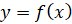 отрицателен. А значит, касательная образует тупой угол с осью 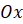. И поэтому график функции на этом промежутке «опускается», то есть функция 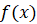 убывает. Сформулируем утверждения.

Если  на промежутке, то функция 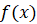 возрастает на этом промежутке.

Если  на промежутке, то функция  убывает на этом промежутке.

А сейчас сформулируем теорему Лагранжа, которую будем использовать при доказательстве теорем о достаточных условиях возрастания или убывания функции.

Итак, если функция 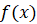 непрерывна на отрезке  и дифференцируема на интервале , то существует точка  такая, что .

Доказательство этой теоремы приводится в курсе высшей математики. Давайте поясним геометрический смысл формулы .

Через точку  и точку  графика  проведём прямую  и назовём её секущей. Построим прямоугольный треугольник , где точка  имеет координаты . Найдём . Он равен отношению .

,  . Тогда .

Угол  равен углу наклона между секущей  и осью 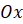. Получается, что угловой коэффициент секущей  равен отношению .

Запишем формулу из теоремы Лагранжа следующим образом: . Это есть угловой коэффициент касательной к графику функции  в точке  с абсциссой .

Таким образом, угловой коэффициент касательной к графику функции в точке  с абсциссой  равен угловому коэффициенту секущей .

Получается, что на интервале  найдётся такая точка , что в точке графика с абсциссой  касательная к графику функции  с параллельна секущей.

Теперь давайте сформулируем теорему о достаточном условии возрастания функции.

Итак, если функция  дифференцируема на интервале   для всех , то функция возрастает на интервале .

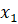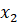Докажем эту теорему с помощью теоремы Лагранжа. Пусть  и  – произвольные точки интервала , такие, что . Применим теорему Лагранжа к отрезку  и получим , .

, ; , так как . Тогда из последней формулы получаем, что , то есть 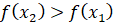. Значит, функция  возрастает на интервале . Таким образом, теорема доказана.

Кроме того, если функция  непрерывна на отрезке  и  на интервале , то эта функция возрастает на отрезке .

Далее сформулируем и докажем с помощью теоремы Лагранжа теорему о достаточном условии убывания функции. Если функция  дифференцируема на интервале  и  для всех , то функция убывает на интервале .

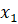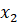Докажем это. Пусть  и  – произвольные точки интервала , такие, что . Применив к отрезку  теорему Лагранжа, получаем , .

, ; , так как . Тогда из последней формулы получаем, что , то есть 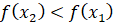. Значит, функция  убывает на интервале . Теорема доказана.

Если функция  непрерывна на отрезке  и  на интервале , то эта функция убывает на отрезке .

Давайте исследуем функцию  на возрастание и убывание.

Отметим, что промежутки возрастания и убывания функции называют промежутками монотонности этой функции.