Прежде чем приступить к рассмотрению новой темы, давайте вспомним,
что функция вида 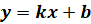 , где
, где 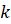 и
и 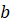 – любые действительные числа, называется линейной.
Графиком этой функции является прямая. Число
– любые действительные числа, называется линейной.
Графиком этой функции является прямая. Число 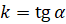 называют угловым коэффициентом прямой, а угол
называют угловым коэффициентом прямой, а угол 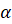 – угол, который эта прямая образует с осью
– угол, который эта прямая образует с осью 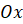 .
.
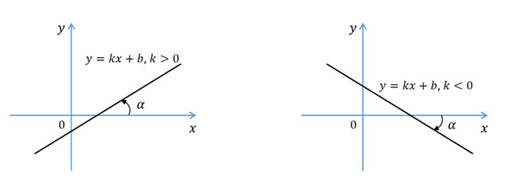
При этом если  , то угол
, то угол 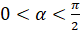 . В этом случае функция возрастает.
. В этом случае функция возрастает.
Если 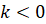 , то угол
, то угол  . В этом случае функция убывает.
. В этом случае функция убывает.
Выясним геометрический смысл производной. Итак, на рисунке
изображён график дифференцируемой функции 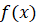 . Пусть точки А и М принадлежат графику этой
функции. Пусть x – абсцисса точки А, x + h – абсцисса точки М. Тогда
. Пусть точки А и М принадлежат графику этой
функции. Пусть x – абсцисса точки А, x + h – абсцисса точки М. Тогда 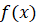 ордината точки А, а f (x + h) ордината точки М. Запишем координаты этих точек.
ордината точки А, а f (x + h) ордината точки М. Запишем координаты этих точек.
Теперь построим треугольник 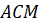 . Он прямоугольный.
. Он прямоугольный.
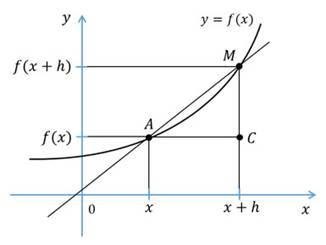
Точка C имеет координаты  . Из этого треугольника найдём угловой коэффициент
. Из этого треугольника найдём угловой коэффициент 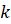 прямой
прямой  . Этот коэффициент зависит от
. Этот коэффициент зависит от  , то есть его можно рассматривать как функцию
, то есть его можно рассматривать как функцию  . Он равен
. Он равен  .
.

 .
.
Тогда  .
.
Пусть число  фиксировано, а
фиксировано, а  . Тогда, посмотрев на рисунок и на координаты точек А и М,
становится понятно, что точка А будет неподвижна, а точка М,
двигаясь по графику, будет стремится к точке А, то есть будет всё ближе
и ближе к ней. При этом прямая АМ будет стремиться занять положение
прямой, которую называют касательной к графику функции
. Тогда, посмотрев на рисунок и на координаты точек А и М,
становится понятно, что точка А будет неподвижна, а точка М,
двигаясь по графику, будет стремится к точке А, то есть будет всё ближе
и ближе к ней. При этом прямая АМ будет стремиться занять положение
прямой, которую называют касательной к графику функции  , так как существует
, так как существует  .
.
Итак,  , то есть тангенсу угла между касательной и осью Оx.
, то есть тангенсу угла между касательной и осью Оx.
Таким образом, геометрический смысл производной состоит в
том, что значение производной функции 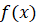 в точке x равно угловому коэффициенту касательной к графику в точке
в точке x равно угловому коэффициенту касательной к графику в точке  .
.
Давайте найдём угол между касательной к графику функции  в точке
в точке  и
и 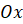 . Для этого найдём угловой коэффициент касательной к графику этой
функции в точке
. Для этого найдём угловой коэффициент касательной к графику этой
функции в точке  . То есть найдём значение производной данной функции при
. То есть найдём значение производной данной функции при  .
.

Давайте найдём угол между касательной к параболе  в точке
в точке  и напишем уравнение этой касательной.
и напишем уравнение этой касательной.

Теперь аналогичным образом выведем уравнение касательной к графику
дифференцируемой функции  в точке
в точке  .
.

Давайте найдём уравнение касательной к графику функции  в точке с абсциссой
в точке с абсциссой  .
.

Здесь угол между касательной к графику функции и осью абсцисс, то
есть  .
.
Сейчас давайте с вами покажем, что касательная к параболе  в точке с абсциссой
в точке с абсциссой  пересекает ось
пересекает ось 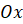 в точке
в точке  .
.

Таким образом, мы показали, что касательная к параболе  в точке с абсциссой
в точке с абсциссой  пересекает ось
пересекает ось 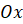 в точке
в точке  .
.
Таким образом, можно сформулировать геометрический способ
построения касательной к параболе  в точке
в точке  с абсциссой
с абсциссой  : прямая, проходящая через точку
: прямая, проходящая через точку  и точку
и точку  оси абсцисс, касается параболы в точке
оси абсцисс, касается параболы в точке  .
.
А сейчас давайте выполним несколько заданий.
Задание первое. Найдите угловой
коэффициент касательной к графику функции  в точке с абсциссой
в точке с абсциссой  :
:
а)  ,
,  ; б)
; б)  ,
,  .
.
Решение.

Задание второе. Найдите угол между
касательной к графику функции  в точке с абсциссой
в точке с абсциссой  и осью
и осью 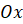 :
:
а)  ,
,  ; б)
; б)  ,
,  .
.
Решение.

Задание третье. Напишите уравнение
касательной к графику функции  в точке с абсциссой
в точке с абсциссой  :
:
а)  ,
,  ; б)
; б)  ,
,  .
.
Решение.


 Получите свидетельство
Получите свидетельство Вход
Вход




 6666
6666

