Производные некоторых элементарных функций

Сегодня на уроке мы повторим правила дифференцирования. Вспомним формулу производной сложной функции. Скажем, какие функции называют элементарными. Познакомимся с производными элементарных функций.

Прежде чем приступить к рассмотрению новой темы, давайте напомним:

,

,

,

,

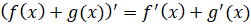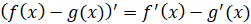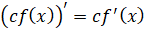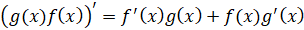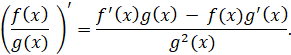
Теперь напомним, что сложная функция – это функция от функции .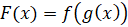

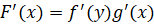, где 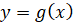, т. е. .

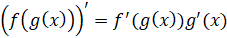Теперь перейдём к рассмотрению производных некоторых элементарных функций.

Элементарными функциями называют степенную, показательную, логарифмическую и тригонометрические функции, а также их различные комбинации.

На одном из предыдущих занятий мы с вами познакомились с формулой производной степенной функции . Эта формула справедлива для любого действительного показателя степени. Она применима при тех значениях , при которых её правая часть имеет смысл.

Приступим к рассмотрению производной показательной функции. Показательная функция , где , , определена на всей числовой прямой и имеет производную в каждой её точке.

Например, , .

Ну а теперь давайте найдём производную функции , где , . Для этого воспользуемся только что рассмотренными формулами.

Так, например, , .

Выясним, как находить производную логарифмической функции , где , .

Например, , .

А сейчас найдём производную функции , где  и . Для этого мы воспользуемся только что рассмотренными формулами.

Перейдём к производным тригонометрических функций. Выведем формулу производной синуса. Обозначим . Найдём . Составим разностное отношение:

Если , то  и .

Воспользуемся утверждением , которое называют первым замечательным пределом и доказывают в курсе высшей математики. Тогда .

Таким образом, .

Следовательно, .

Выведем формулу производной косинуса. Обозначим . Найдём производную этой функции. Составим разностное отношение.

Если , то  и .

Тогда .

Следовательно, .

Таким образом, мы доказали формулу производной синуса и формулу производной косинуса. Также справедливы следующие две формулы:

, .

Их можно доказать, применив правило дифференцирования сложной функции.

Давайте найдём производную функции .

И найдём производную .

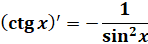
Давайте выполним задание. Найдите производные функций:

а) ; б) ; в) .

Решение.

Задание второе. Найдите производные функций:

а) ; б) .

Решение.