Правила дифференцирования

Сегодня на уроке мы повторим определение производной функции. Вспомним известные формулы производных. Познакомимся с правилами дифференцирования суммы, произведения и частного. Познакомимся с формулой нахождения производной сложной функции.

Прежде чем приступить к рассмотрению новой темы, давайте напомним определение производной.

Пусть функция 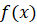 определена на некотором промежутке,  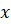– точка этого промежутка и число  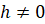такое, что  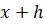также принадлежит данному промежутку. Тогда предел разностного отношения 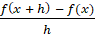 при 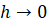 (если этот предел существует), называется производной функции  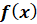в точке  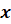и обозначается 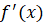. Таким образом, .

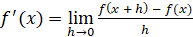Вспомним, что , , , .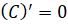

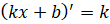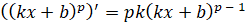Теперь приступим к рассмотрению правил дифференцирования.  

Итак, производная суммы равна сумме производных, то есть .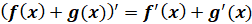

Это свойство производной можно сформулировать так: если каждая из функци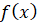й  и 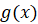 имеет производную, то их сумма также имеет производную и справедлива данная формула.

Давайте докажем эту формулу, используя определение производной.

Производная разности равна разности производных, то есть .

Отметим, что производная суммы нескольких функций равна сумме производных этих функций.

Давайте найдём производную функции .

.

Следующее правило дифференцирования. Постоянный множитель можно вынести за знак производной: .

Найдём производную функции .

Познакомимся с ещё двумя правилами дифференцирования.

Производная произведения двух функций равна сумме произведения производной первого множителя на второй множитель и произведения первого множителя на производную второго множителя.

Отметим, что эта формула справедлива при условии, что функци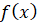и  и 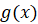 имеют производную в точке .

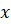Найдём производную функции .

И познакомимся с ещё одной формулой, которую используют для нахождения производной частного. Производная частного двух функций равна дроби, у которой знаменатель есть квадрат знаменателя данной дроби, а числитель представляет собой разность произведения производной числителя на знаменатель и произведения числителя на производную знаменателя.

Эта формула справедлива при условии, что функции 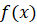 и  имеют производную в точке 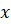, причём функция .

Найдём производную функции .

Сейчас давайте поговорим о производной сложной функции.

Посмотрите на функцию . Данную функцию можно рассматривать как сложную функцию , где .

Получается, что  – это функция, аргументом которой является функция .

Таким образом, сложная функция – это функция от функции .

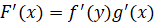, где .

Найдём производную функции .

А сейчас давайте выполним задание. Найдите производные следующих функций.

а) ; б) ; в) .

Решение.