Сегодня на уроке мы вспомним определение производной функции. Познакомимся с формулой производной степенной функции.
Прежде чем приступить к рассмотрению новой темы, давайте вспомним определение производной.
Итак, пусть функция 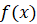 определена на некотором промежутке,
определена на некотором промежутке, 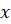 – точка этого промежутка и число
– точка этого промежутка и число 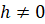 такое, что
такое, что 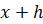 также принадлежит данному промежутку. Тогда предел разностного
отношения
также принадлежит данному промежутку. Тогда предел разностного
отношения 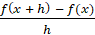 при
при 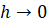 (если этот предел существует), называется производной функции
(если этот предел существует), называется производной функции 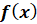 в точке
в точке 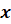 и обозначается
и обозначается 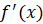 . Таким образом,
. Таким образом, 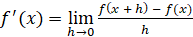 .
.
Давайте с вами докажем, что 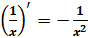 .
.

Сейчас докажем, что 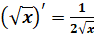 .
.

На предыдущем занятии мы с вами получили следующие формулы для производных:
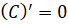 ;
; 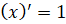 ;
; 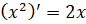 ;
; 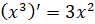 .
.
На этом занятии мы доказали, что 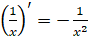
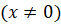 ,
, 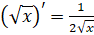
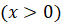 .
.
Четыре последние формулы являются формулами производной степенной
функции 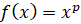 для
для 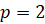 , для
, для 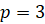 , для
, для 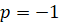 и для
и для 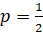 .
.
Заметим, что эти четыре формулы мы можем записать следующим образом:
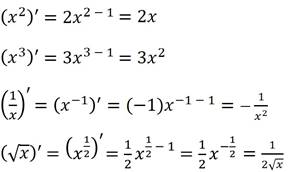
Ещё раз посмотрев на каждую из формул, сделаем вывод, что для
любого действительного показателя справедлива формула производной степенной
функции: 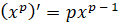
Приведём примеры.
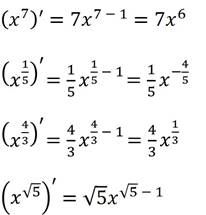
Познакомимся с ещё одной формулой. Если нам с вами надо найти
производную 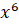 , то мы воспользуемся формулой производной степенной функции и
получим
, то мы воспользуемся формулой производной степенной функции и
получим 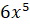 . Если надо найти
. Если надо найти 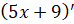 , то мы воспользуемся известной вам формулой
, то мы воспользуемся известной вам формулой 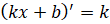 и в результате получим
и в результате получим 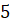 .
.
Но бывают более сложные случаи. Например, нам надо найти 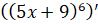 . Здесь мы можем воспользоваться вот такой формулой
. Здесь мы можем воспользоваться вот такой формулой 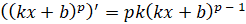 .
.
В нашем случае 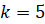 ,
, 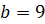 ,
, 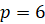 . Тогда по этой формуле получаем, что
. Тогда по этой формуле получаем, что 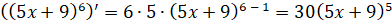 .
.
А сейчас давайте выполним несколько заданий.
Задание первое. Найдите производные функций:
а) 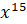 ; б)
; б) 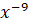 ; в)
; в) 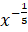 ; г)
; г) 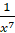 ; д)
; д) 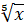 ; е)
; е) 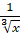 .
.
Решение.
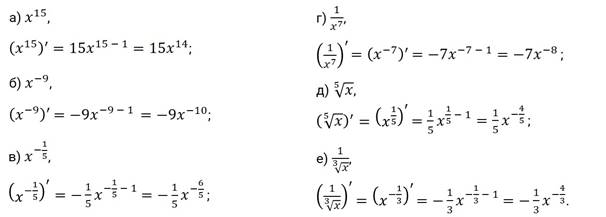
Задание второе. Найдите производные функций:
а) 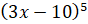 ; б)
; б) 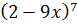 ; в)
; в) 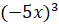 ; г)
; г) 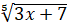 ; д)
; д) 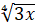 .
.
Решение.
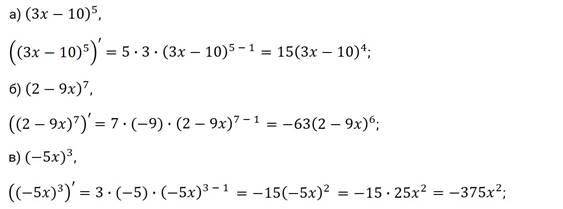
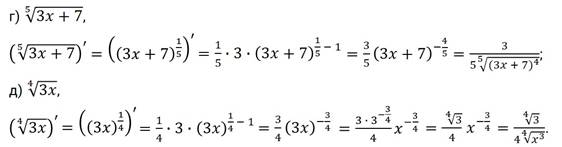
Задние третье. Найдите 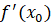 , если:
, если:
а) 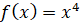 ,
, 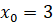 ; б)
; б) 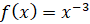 ,
, 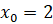 ; в)
; в) 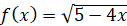 ,
, 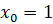 .
.
Решение.
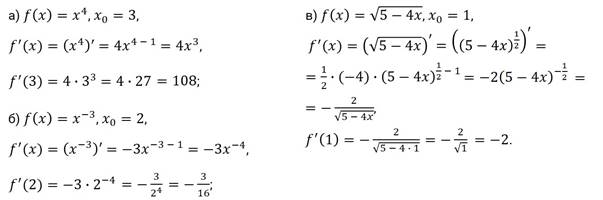

 Получите свидетельство
Получите свидетельство Вход
Вход




 7518
7518

