Производная

Сегодня на уроке мы поговорим о мгновенной скорости. Введём понятие производной функции. Сформулируем определение предела функции. Скажем, какие функции называют непрерывными на некотором промежутке. Сформулируем строгое определение непрерывности функции.

Давайте с вами решим задачу. Поезд, двигаясь равнозамедленно с ускорением 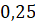 м/c², проходит  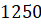м и останавливается. Определите скорость поезда в момент начала торможения.

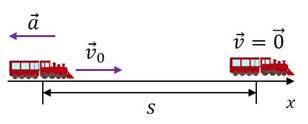
Итак, нам надо найти скорость в момент начала торможения, то есть мгновенную скорость в этот момент времени.

Воспользуемся формулами из курса физики:

.

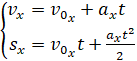Теперь учтём, что проекция ускорения на ось x отрицательная (так как поезд двигается равнозамедленно), а конечная скорость поезда равна нулю. Нам надо найти 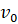 (скорость в момент начала торможения).

Подставим в систему уравнений известные из условия значения пути и ускорения. Решим её.

Отметим, что от мгновенной скорости зависит решение многих практических задач.

При нахождении мгновенной скорости используется средняя скорость движения за малый промежуток времени.

Давайте рассмотрим, как связаны между собой средняя и мгновенная скорости движения.

Итак, пусть материальная точка  движется вдоль оси , где О – положение этой точки в момент времени t = 0. Если в момент времени t координата материальной точки равна , где , то функцию  называют законом движения точки .

При неравномерном движении материальная точка за равные по длительности промежутки времени может совершать перемещения, разные как по величине, так и по направлению. За промежуток времени от  до  средняя скорость движения материальной точки определяется как , .

Если рассматриваемое движение не является равномерным, то средняя скорость при фиксированном  будет меняться при изменении . При этом чем меньше будет , тем точнее средняя скорость будет характеризовать движение точки в момент времени .

Скоростью точки в момент времени  (мгновенной скоростью) называют предел, к которому стремится средняя скорость, когда , то есть скорость в момент времени  определяется равенством .

Таким образом, получается, что скорость в момент времени  – это предел отношения приращения координаты  за промежуток времени от  до  к приращению времени  при , если этот предел существует.

Так, например, пусть материальная точка движется по закону свободного падения .

Тогда .

Откуда , то есть .

Отношение  называют разностным отношением, а его предел  – производной функции  и обозначают .

Итак, пусть функция  определена на некотором промежутке.  – точка этого промежутка и число , такое, что  также принадлежит данному промежутку. Тогда предел разностного отношения  при  (если такой предел существует) называется производной функции  в точке  и обозначается .

Отметим, что в этой формуле число  может быть и положительным, и отрицательным, при этом число  должно принадлежать промежутку, на котором определена функция .

Если функция  имеет производную в точке , то она называется дифференцируемой в точке .

Если функция  имеет производную в каждой точке некоторого промежутка, то говорят, что она дифференцируема на этом промежутке.

Давайте найдём производную функции .

Давайте найдём производную функции , где  – заданное число. Составим разностное отношение.

Получается, что оно равно 0 при любом , то есть его значение не меняется .

Таким образом, производная постоянной равна нулю.

Давайте выясним, чему равна производная линейной функции .

Составим разностное отношение.

Разностное отношение равно  при любом , тогда предел этого отношения при  равен .

Следовательно, .

Например, , , .

Так как изучение теории пределов не входит в программу средней школы, то в школьном курсе математики некоторые формулы производных строго не доказываются или вообще принимаются без доказательства.

При нахождении производных простейших функций мы пользуемся наглядными представлениями. Например, считаем наглядно понятным, что если , то , , .

Но несмотря на это, мы всё же приведём строгое определение предела функции в точке.

Число А называется пределом функции  в точке  и обозначается , если для любого числа  существует такое число , что для всех , удовлетворяющих условию , где , выполняется неравенство .

Давайте поясним это определение. Число А является пределом функции  в точке , если значения  при , достаточно близких к , становятся как угодно близкими к числу А, то есть значения  становятся как угодно малыми.

Это означает, что можно взять сколь угодно малое положительное число  и убедиться в том, что для всех , отличающихся от  меньше, чем на некоторое число , .

Например, если , то .

Поэтому для всех , таких, что , где , справедливо неравенство .

Так, например, если , то .

Понятие предела функции тесно связано с понятием непрерывности.

Если график функции представляет собой непрерывную линию на некотором промежутке, то эту функцию называют непрерывной на этом промежутке.

Все элементарные функции (линейная, квадратичная, тригонометрические и другие), которые мы изучаем в школьном курсе математики, являются непрерывными на каждом промежутке, на котором они определены.

На следующем рисунке изображён график функции , которая не является непрерывной. Она непрерывна на промежутках  и .

Но она разрывна в точке . Поэтому она не является непрерывной на отрезке .

Сформулируем строгое определение непрерывности функции. Функция  называется непрерывной в точке , если .

Если функция непрерывна в каждой точке некоторого интервала, то её называют непрерывной на этом интервале.

Например, функция , график которой мы рассмотрели, непрерывна на интервале , а вот на интервале  она не является непрерывной.

Отметим, что если функция имеет производную на некотором интервале, то на этом интервале она непрерывна. А вот обратное утверждение неверно. То есть непрерывная на промежутке функция может не иметь производную в некоторых точках этого промежутка.

А сейчас давайте выполним задание. Используя определение производной, найдите , если:

а) ; б) .

Решение.