Сегодня на уроке мы с вами поговорим о функции 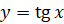 . Познакомимся с графиком функции
. Познакомимся с графиком функции 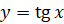 . А также рассмотрим основные свойства этой функции.
. А также рассмотрим основные свойства этой функции.
Прежде чем приступить к рассмотрению новой темы, давайте напомним,
что областью определения функции 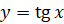 является множество действительных чисел, кроме
является множество действительных чисел, кроме 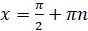 ,
, 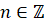 . Множеством значений функции является множество действительных
чисел. Также мы знаем, что функция
. Множеством значений функции является множество действительных
чисел. Также мы знаем, что функция 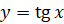 является нечётной и периодической с периодом
является нечётной и периодической с периодом 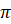 .
.
Известно, что график нечётной функции симметричен относительно
начала координат. Поэтому мы построим график функции 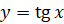 на промежутке
на промежутке 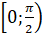 , а затем отразим его относительно начала координат и получим график
на интервале
, а затем отразим его относительно начала координат и получим график
на интервале 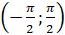 .
.
Прежде чем начать строить график функции на промежутке 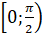 , покажем, что на этом промежутке функция
, покажем, что на этом промежутке функция 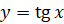 возрастает.
возрастает.
Пусть 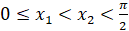 . Покажем, что
. Покажем, что 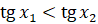 , то есть
, то есть 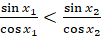 .
.
По условию и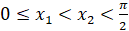 .
. 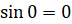 ,
,  входит в указанный промежуток. А также по свойству возрастания
функции
входит в указанный промежуток. А также по свойству возрастания
функции 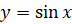 имеем
имеем 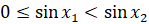 .
.
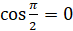 ,
,  не входит в указанный промежуток. А также по свойству убывания
функции
не входит в указанный промежуток. А также по свойству убывания
функции 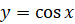 имеем
имеем 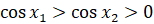 , откуда
, откуда 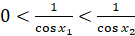 .
.
Теперь, перемножив неравенство 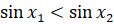 и неравенство
и неравенство 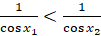 , получим, что
, получим, что 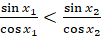 . Таким образом, мы показали, что функция
. Таким образом, мы показали, что функция 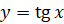 возрастает на промежутке
возрастает на промежутке 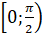 .
.
Зная это, найдём координаты нескольких точек графика функции 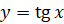 . Заполним таблицу.
. Заполним таблицу.

Отметив полученные точки на координатной плоскости, построим
график функции 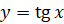 на промежутке
на промежутке 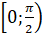 . Теперь отразим построенный график относительно начала координат
и получим график на интервале
. Теперь отразим построенный график относительно начала координат
и получим график на интервале 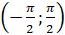 .
.

Мы знаем, что  и при
и при  функция
функция 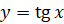 не определена.
не определена.
Если  и
и  приближается к
приближается к  , то
, то  приближается к 1, а
приближается к 1, а  , оставаясь положительным, приближается к 0. При этом дробь
, оставаясь положительным, приближается к 0. При этом дробь  , равная
, равная  , неограниченно возрастает, и поэтому график функции
, неограниченно возрастает, и поэтому график функции 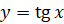 приближается к вертикальной прямой
приближается к вертикальной прямой  .
.
Аналогичным образом при отрицательных значениях  , больших
, больших  и приближающихся к
и приближающихся к  , график функции
, график функции 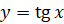 приближается к вертикальной прямой
приближается к вертикальной прямой  .
.
Прямые  и
и  являются вертикальными асимптотами графика функции
являются вертикальными асимптотами графика функции 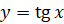 .
.
Функция 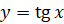 периодическая с периодом
периодическая с периодом 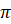 . Тогда её график на всей области определения получается из
графика на интервале
. Тогда её график на всей области определения получается из
графика на интервале 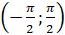 сдвигами вдоль оси абсцисс на
сдвигами вдоль оси абсцисс на  ,
, 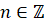 .
.
Так, весь график рассматриваемой функции строится с помощью
геометрических преобразований его части, которую мы построили на промежутке 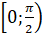 .
.
График функции 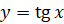 называется тангенсоидой.
называется тангенсоидой.
А сейчас давайте поговорим об основных свойствах функции  .
.
Итак, область определения функции – множество действительных
чисел, кроме 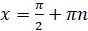 ,
, 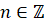 . Множество значений – множество всех действительных чисел. Функция
периодическая с периодом
. Множество значений – множество всех действительных чисел. Функция
периодическая с периодом  . Нечётная.
. Нечётная.
Функция 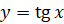 принимает значение, равное 0, при
принимает значение, равное 0, при  ,
, 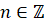 .
.
Положительные значения функция принимает на интервалах  ,
, 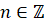 , а отрицательные – на интервалах
, а отрицательные – на интервалах  ,
, 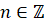 .
.
Функция 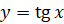 возрастает на любом интервале
возрастает на любом интервале  ,
, 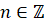 .
.
А сейчас давайте выполним несколько заданий.
Задание первое. Найдите все корни
уравнения  , принадлежащие отрезку
, принадлежащие отрезку  .
.
Решение.

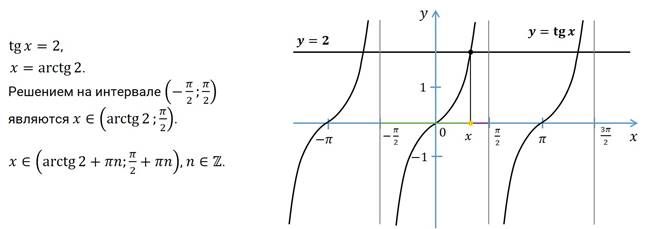
Задание второе. Найдите все решения
неравенства  , принадлежащие отрезку
, принадлежащие отрезку  .
.
Решение.

Задание третье. Решите неравенство  .
.
Решение.

 Получите свидетельство
Получите свидетельство Вход
Вход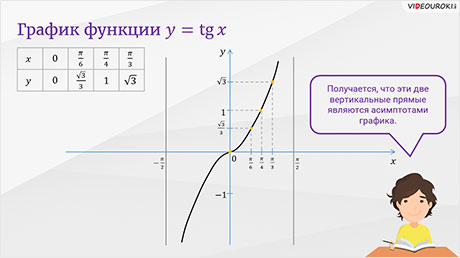




 3304
3304

