Сегодня на уроке мы с вами поговорим о функции 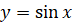 . Познакомимся с графиком функции
. Познакомимся с графиком функции 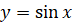 . А также рассмотрим основные свойства этой функции.
. А также рассмотрим основные свойства этой функции.
Прежде чем приступить к рассмотрению новой темы, давайте напомним,
что функция 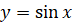 определена на всей числовой прямой, а множеством её значений
является отрезок
определена на всей числовой прямой, а множеством её значений
является отрезок 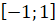 . Значит, эта функция ограничена и её график расположен в полосе
между прямыми
. Значит, эта функция ограничена и её график расположен в полосе
между прямыми  и
и 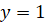 . Также мы знаем, что функция
. Также мы знаем, что функция 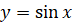 является нечётной и периодической с периодом
является нечётной и периодической с периодом 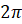 . Её график можно построить таким же образом, как мы строили
график функции
. Её график можно построить таким же образом, как мы строили
график функции 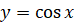 , также начиная построение, например, на отрезке
, также начиная построение, например, на отрезке 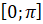 , а затем распространив график по всей числовой прямой с помощью
сдвигов. Но давайте с вами поступим следующим образом.
, а затем распространив график по всей числовой прямой с помощью
сдвигов. Но давайте с вами поступим следующим образом.
Вспомним формулу приведения 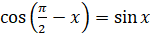 .
.
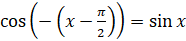 ,
, 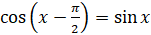 ,
, 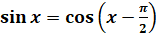 .
.
Известно, что график функции 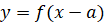 , где
, где 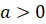 , получается из графика функции
, получается из графика функции 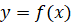 сдвигом вдоль оси абсцисс на
сдвигом вдоль оси абсцисс на 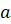 единиц вправо.
единиц вправо.
Таким образом, мы получили формулу, которая показывает, что график
функции 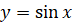 можно получить сдвигом графика функции
можно получить сдвигом графика функции 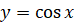 вдоль оси абсцисс вправо на
вдоль оси абсцисс вправо на  .
.

Кривая, являющаяся графиком функции 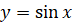 , называется синусоидой.
, называется синусоидой.
График функции  хорошо иллюстрирует её свойства. Давайте поговорим об основных
свойствах функции.
хорошо иллюстрирует её свойства. Давайте поговорим об основных
свойствах функции.
Итак, мы уже знаем, что область определения функции – множество
всех действительных чисел, а множество значений – отрезок 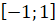 .
.
Функция нечётная. Её график симметричен относительно начала
координат. Данная функция периодическая с периодом  .
.
Функция принимает значение, равное  , при
, при  ,
,  .
.
Функция принимает наибольшее значение 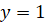 при
при  ,
,  , а наименьшее значение
, а наименьшее значение  при
при  ,
,  .
.
 при
при  ,
,  .
.
 при
при  ,
,  .
.
Возрастает функция на отрезках  ,
,  .
.
Убывает функция на отрезках  ,
,  .
.
А сейчас давайте выполним несколько заданий.
Задание первое. Найдите все корни
уравнения  , принадлежащие отрезку
, принадлежащие отрезку  .
.
Решение.

Задание второе. Найдите все решения
неравенства  , принадлежащие отрезку
, принадлежащие отрезку  .
.
Решение.

Задание третье. Выразив косинус через синус по формулам приведения, сравните числа:
а)  и
и  ; б)
; б)  и
и  ; в)
; в)  и
и  ; г)
; г)  и
и  .
.
Решение.



 Получите свидетельство
Получите свидетельство Вход
Вход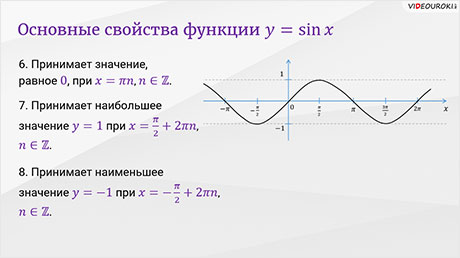




 4918
4918

