Сегодня на уроке мы с вами поговорим о функции 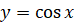 . Рассмотрим график функции
. Рассмотрим график функции 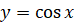 , а также основные свойства этой функции.
, а также основные свойства этой функции.
Прежде чем приступить к рассмотрению новой темы, давайте напомним,
что функция 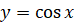 определена на всей числовой прямой, а множеством её значений
является отрезок
определена на всей числовой прямой, а множеством её значений
является отрезок 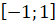 . Функция
. Функция 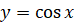 ограничена и её график расположен в полосе между прямыми
ограничена и её график расположен в полосе между прямыми 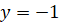 и
и 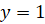 .
.
Также мы знаем, что функция 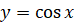 периодическая с периодом
периодическая с периодом 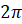 , а значит, достаточно построить её график на промежутке длиной
, а значит, достаточно построить её график на промежутке длиной 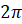 . Например, на отрезке
. Например, на отрезке  .
.
На предыдущем уроке мы с вами выяснили, что функция 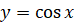 является чётной. Известно, что график чётной функции симметричен
относительно оси ординат.
является чётной. Известно, что график чётной функции симметричен
относительно оси ординат.
Тогда для построения графика на отрезке  нам достаточно построить его на отрезке
нам достаточно построить его на отрезке 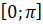 , а затем симметрично отразить относительно оси Oy.
, а затем симметрично отразить относительно оси Oy.
Прежде чем мы перейдём к построению графика, покажем, что функция 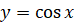 убывает на отрезке
убывает на отрезке 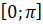 .
.
Давайте на единичной окружности с центром в начале координат
отметим точку 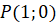 . Тогда при повороте точки
. Тогда при повороте точки 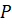 вокруг начала координат против часовой стрелки на угол
вокруг начала координат против часовой стрелки на угол 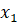 получим точку
получим точку 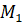 . Абсцисса этой точки –
. Абсцисса этой точки – 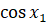 .
.
При повороте точки 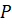 вокруг начала координат против часовой стрелки на угол
вокруг начала координат против часовой стрелки на угол  получим точку
получим точку  . Абсцисса этой точки –
. Абсцисса этой точки –  .
.
Обратите внимание, что при повороте точки 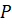 вокруг начала координат против часовой стрелки на угол от
вокруг начала координат против часовой стрелки на угол от  до
до  абсцисса точки, то есть
абсцисса точки, то есть  , уменьшается от
, уменьшается от  до
до  . Поэтому если
. Поэтому если  , то
, то  . Это значит, что функция
. Это значит, что функция 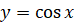 убывает на отрезке
убывает на отрезке 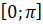 .
.

Теперь давайте найдём координаты некоторых точек графика функции 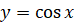 и заполним таблицу значений функции.
и заполним таблицу значений функции.

Используя свойство убывания функции 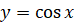 и отметив полученные точки на координатной плоскости, построим
график функции на отрезке
и отметив полученные точки на координатной плоскости, построим
график функции на отрезке 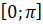 .
.
Так как функция игрек равно косинус икс является чётной, то мы
можем отразить построенный на отрезке 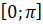 график симметрично относительно оси Oy. В результате получим график
этой функции на отрезке
график симметрично относительно оси Oy. В результате получим график
этой функции на отрезке  .
.

Длина этого отрезка равна 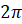 , то есть равна периоду функции. А значит, мы можем распространить
график по всей числовой прямой с помощью сдвигов на
, то есть равна периоду функции. А значит, мы можем распространить
график по всей числовой прямой с помощью сдвигов на 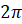 ,
,  и так далее вправо и на
и так далее вправо и на 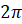 ,
,  и так далее влево, то есть на
и так далее влево, то есть на  ,
,  .
.
Получается, что мы геометрически построили график функции 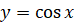 на всей числовой прямой, начав с построения его части на отрезке
на всей числовой прямой, начав с построения его части на отрезке 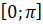 .
.
Тогда свойства рассматриваемой функции можно получить, опираясь на
её свойства на отрезке 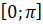 .
.
Так, например, мы выяснили, что функция 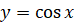 убывает на отрезке
убывает на отрезке 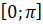 и является чётной, а значит, на отрезке
и является чётной, а значит, на отрезке  она возрастает.
она возрастает.
А сейчас давайте поговорим об основных свойствах функции  .
.
Вы уже знаете, что область определения функции – множество  всех действительных чисел.
всех действительных чисел.
Множество значений – отрезок 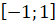 .
.
Функция является чётной, то есть  .
.
График функции симметричен относительно оси ординат.
Функция периодическая с периодом  .
.
Функция принимает значение, равное  , при
, при  ,
,  .
.
Наибольшее значение 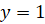 функция принимает при
функция принимает при  .
.
Наименьшее значение 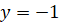 функция принимает при
функция принимает при  ,
, .
.
 при
при  ,
,  .
.
 при
при  ,
,  .
.
Возрастает функция на отрезках  ,
,  .
.
Убывает функция на отрезках  ,
,  .
.
А сейчас давайте выполним несколько заданий.
Задание первое. Найдите все корни уравнения
 , принадлежащие отрезку
, принадлежащие отрезку  .
.
Решение.

Задание второе. Найдите все решения
неравенства  , принадлежащие отрезку
, принадлежащие отрезку  .
.
Решение.


 Получите свидетельство
Получите свидетельство Вход
Вход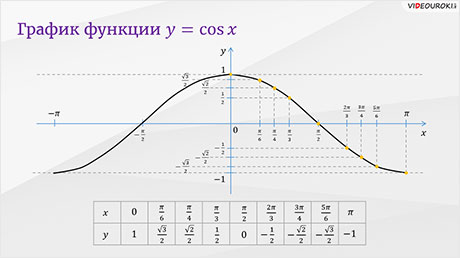




 9239
9239

