Показательная функция, её свойства и график

Если каждому значению из некоторого множества действительных чисел поставлено в соответствие по определённому правилу число, то говорят, что на этом множестве определена функция.

При этом   называют независимой переменной или аргументом, а – зависимой переменной или функцией.

Множество значений, для которых определены значения , называют областью определения функции.

Мы с вами уже говорили, что степень определена для любого положительного основания и любого действительного показателя.

Давайте вспомним основные свойства степени.

Пусть , , ,  и   — любые действительные числа. Тогда верны следующие равенства:

;

;

;

;

;

;

, если , ;

, если , ;

, если , .

Понятие степени с действительным показателем позволяет нам рассматривать функции вида .

Итак, пусть основание степени . Тогда каждому  соответствует одно определённое число . То есть тем самым задана функция .

В случае если , то функция  принимает одно и то же значение  при всех . Этот случай нас интересовать не будет.

Запомните! Показательной функцией называется функция вида , где  — заданное число, , .

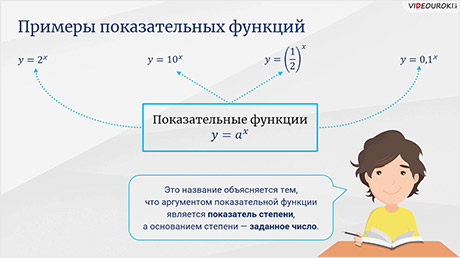
Например, функции ‚ ‚ ,  и так далее – это показательные функции.

То есть имеем дело с функциями вида , где а — заданное положительное число, х — переменная. Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.

Как же будет выглядеть график такой функции?

Итак, давайте построим график функции , например, при а = 2. Для этого, как обычно, найдём сначала координаты некоторых точек графика и заполним таблицу значений функции.

Отметим эти точки на координатной плоскости и соединим.

Получившаяся кривая является графиком функции , аргумент которой может принимать любые действительные значения. Отметим, что график функции  проходит через точку с координатами , и расположен выше оси . Если  и   увеличивается, то график быстро приближается к оси , но не пересекает её. Таким образом, ось  является горизонтальной асимптотой графика функции .

Если  и   увеличивается, то график быстро поднимается вверх. Такой же вид имеет график любой функции , если .

Если же основание степени , а точнее , то график функции будет симметричен относительно оси ординат.

Например, нам нужно построить график функции . Поскольку , то график функции  мы можем получить из графика функции  с помощью симметрии относительно оси ординат.

Заметим, что график этой функции также проходит через точку с координатами (0;1) и расположен выше оси . Если  и  увеличивается, то график быстро приближается к оси , не пересекает её. Таким образом, ось  является горизонтальной асимптотой графика функции . Если  и  увеличивается, то график быстро поднимается вверх. Такой же вид имеет график любой функции и, если .

Рассматривая эти графики, мы можем отметить несколько свойств, общих для всех функций вида .

1. Область определения показательной функции — множество  всех действительных чисел.

Это свойство следует из того, что , где , определена для всех действительных .

2. Множество значений показательной функции — множество всех положительных чисел.

3. Показательная функция  является возрастающей на множестве всех действительных чисел, если , и убывающей, если .

А теперь давайте приступим к практической части нашего урока.

Задание. Решите уравнение .

Решение. Введём вспомогательную переменную .

Ответ: .