Конденсатор — устройство, предназначенное для накопления электрического заряда и энергии электрического поля. Прообразом всех современных конденсаторов была лейденская банка, изобретённая в 1745 году Питером ван Мушенбруком.
После того как лейденской банке научились сообщать большой заряд с помощью электростатической машины, началось подробное изучение её электрического разряда. Так, замыкая обкладки лейденской банки на катушку со стальным сердечником, было обнаружено намагничивание последнего. С одной стороны, в этом нет ничего удивительного, ведь мы знаем, что электрический ток порождает магнитное поле, которое, собственно, и намагничивает сердечник. Интересно было другое. Невозможно было предсказать, какой конец сердечника катушки окажется северным полюсом, а какой — южным.
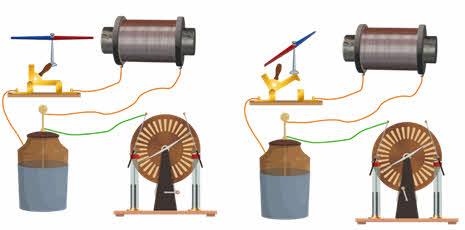
Далеко не сразу поняли, что при разрядке конденсатора через катушку в электрической цепи возникают колебания, названные позже электромагнитными. Поэтому за время разрядки конденсатора ток в цепи много раз меняет направление. В результате этого сердечник и намагничивался каждый раз по-разному.
В настоящее время под электромагнитными колебаниями понимают периодические изменения заряда, напряжения и силы тока в электрической цепи.
Система, в которой могут происходить свободные электромагнитные колебания, называется колебательным контуром.
Простейший колебательный контур представляет собой электрическую цепь из последовательно соединённых катушки индуктивности и конденсатора.
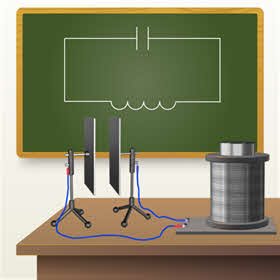
Давайте получим электромагнитные колебания. Для чего соберём цепь, состоящую из источника постоянного тока, катушки индуктивности с большим числом витков, на которую в средней её части, поверх первичной обмотки намотана вторичная обмотка с малым числом витков, и ключа. Вторичную обмотку катушки замкнём на гальванометр, с помощью которого будем регистрировать возникновение колебаний в контуре. Зарядим конденсатор, подключив его на некоторое время к источнику тока. А теперь перекинем ключ: стрелка гальванометра начала совершать колебания, фиксируя наличие переменного тока в катушке.
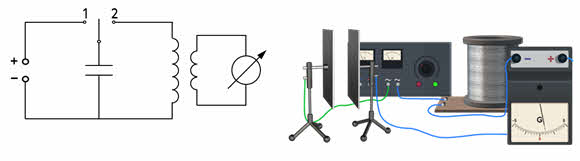
Если в такую цепь параллельно катушке включить электронный осциллограф, то на его экране мы получим временную развёртку колебаний, подобную той, что вычерчивает пружинный маятник на движущемся листе бумаги. Как видим, эти колебания затухают с течением времени. Поэтому они являются свободными.
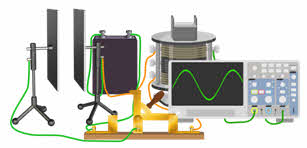
Теперь давайте подробно рассмотрим процесс разрядки конденсатора и проследим за происходящими превращениями энергии. Итак, пусть в начальный момент времени наш конденсатор заряжен, а между его обкладками существует электрическое поле:
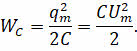
Эта ситуация эквивалентна ситуации с механическими колебаниями математического маятника и соответствует состоянию, когда его вывели из положения равновесия, тем самым сообщив потенциальную энергию.
При замыкании цепи, конденсатор начнёт разряжаться, под действием электрического поля заряды начнут двигаться по виткам катушки, создавая в цепи ток, сила которого постепенно увеличивается. В результате, как мы знаем, в катушке возникнет ток самоиндукции, противодействующий росту тока во внешней цепи. По мере разрядки конденсатора электрическое поле в нём будет ослабевать, а в катушке возникнет магнитное поле. При этом уменьшение энергии электростатического поля конденсатора равно увеличению энергии магнитного поля катушки:
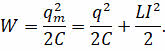
В тот момент, когда конденсатор полностью разрядится, магнитное поле катушки будет самым сильным. Это означает, что энергия электрического поля конденсатора полностью перейдёт в энергию магнитного поля катушки:
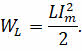
Похожее происходит и с математическим маятником, при прохождении им положения равновесия, когда потенциальная энергия маятника полностью переходит в его кинетическую энергию.
Хотя в этот момент электрическое поле в конденсаторе отсутствует, заряды некоторое время будут двигаться в цепи в прежнем направлении по инерции. Сила тока в цепи начнёт постепенно уменьшаться, так как ток самоиндукции меняется на противоположный, поддерживающий убывающий ток в цепи.
В результате конденсатор снова зарядится, но заряды обкладок поменяются местами. Ток на мгновение прекратится и вся энергия магнитного поля катушки превратиться обратно в энергию электрического поля конденсатора.
Эта ситуация эквивалентна ситуации с механическими колебаниями, в момент отклонения маятника от положения равновесия в противоположную сторону, когда его кинетическая энергия полностью переходит в потенциальную.
Далее явление повторится в обратном порядке: конденсатор начнёт разряжаться и энергия его электрического поля будет преобразовываться в энергию магнитного поля катушки индуктивности. Но в этом случае через катушку течёт ток противоположного направления. Сила тока в катушке вновь достигнет своего максимального значения, когда конденсатор полностью разрядится. А значит, вся электрическая энергия превратится в энергию магнитного поля, аналогично тому, как маятник, возвращаясь, вновь проходит положение своего равновесия, и его потенциальная энергия полностью переходит в кинетическую.
После этого сила тока начинает уменьшаться, а конденсатор будет перезаряжаться. Когда ток в цепи прекратиться, конденсатор окажется заряженным так, как в начальный момент времени. Теперь опять вся энергия колебательного контура заключена в его электрическом поле, вторая перезарядка возвращает контур в исходное состояние. Эта ситуация аналогично тому, как маятник возвращается в своё исходное положение, а его кинетическая энергия полностью переходит в потенциальную.

Таким образом, завершилось полное колебание в контуре, и в дальнейшем процесс повторяется в уже рассмотренной нами последовательности. Минимальный промежуток времени, через который процесс в колебательном контуре полностью повторяется, называют периодом электромагнитных колебаний.
Как вы могли заметить, если в контуре отсутствует активное сопротивление, то его полная энергия сохраняется неизменной и её значение в любой момент времени равно либо максимальной энергии электрического поля, либо максимальной энергии поля магнитного:
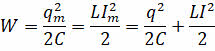
Почему при рассмотрении процессов, происходящих в колебательном контуре, мы их сравнивали с колебаниями математического маятника? Дело в том, что эти процессы описываются одинаковыми уравнениями, что позволяет переносить закономерности, полученные при изучении одного вида колебаний, на колебания другой природы.
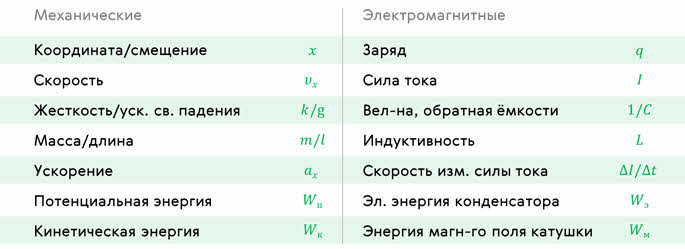
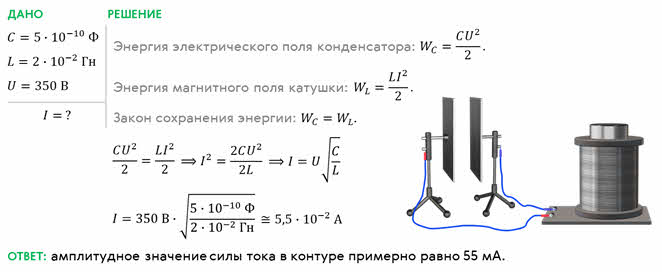
Для закрепления материала, решим с вами такую задачу: колебательный контур состоит из конденсатора ёмкостью 500 пФ и катушки, индуктивностью 20 мГн. Определите амплитудное значение силы тока в контуре, если амплитудное значение напряжения на конденсаторе составляет 350 В.
В заключение отметим ещё одну важную особенность электромагнитных колебаний: если не пополнять извне заряды на обкладках конденсатора, то колебания довольно быстро прекратятся, так как проводники обладают сопротивлением. При протекании в них тока, они нагреваются, на что расходуется энергия контура. Чтобы колебания не прекращались, необходимо к конденсатору подключить источник тока, напряжение которого изменяется периодически с определённой частотой, который и будет вбрасывать внутрь цепи новые порции энергии, не давая ей израсходоваться полностью. В этом случае в контуре будут существовать вынужденные электромагнитные колебания, происходящие с частотой, равной частоте изменения напряжения источника тока. Однако если частота переменного напряжения совпадёт с собственной частотой колебаний контура, то в цепи произойдёт резкое увеличение силы тока — возникнет резонанс. Это явление широко применяется в радиотехнике.

 Получите свидетельство
Получите свидетельство Вход
Вход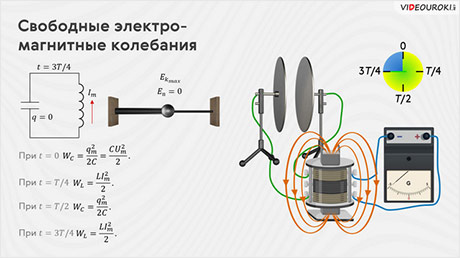




 8864
8864

