Одночлен

Вопросы занятия:

·  вспомнить, что называют одночленом;

·  вспомнить, как одночлены приводить к стандартному виду;

·  поговорить о коэффициентах и степенях одночленов;

· вспомнить, какие одночлены являются подобными.

Материал урока

Для начала давайте вспомним, что же называют одночленом.

Определение.

Одночленом называется произведение чисел и степеней переменных с натуральными показателями.

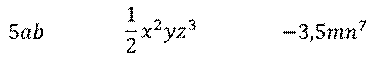
Числа и степени переменных также считаются одночленами.

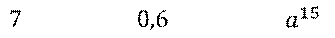
А вот число 0 (нуль) называется нулевым одночленом.

Задание.

На экране записаны следующие выражения:

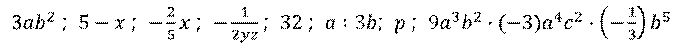
Давайте выберем какие из указанных выражений являются одночленами, а какие – нет. Будем поочерёдно рассматривать каждое выражение.

Решение:

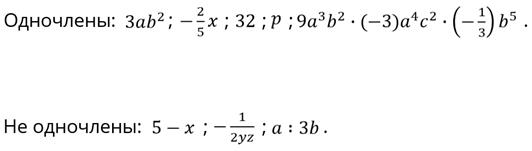
Обратите внимание, в последнем одночлене мы можем перемножить между собой числа и степени с одинаковыми основаниями. Следовательно, очень важную роль при работе с одночленами играют известные вам теоремы о степенях.

Вспомним их. Это умножение и деление степеней с одинаковыми основаниями, возведение в степень, а также умножение и деление степеней с одинаковыми показателями, но с разными основаниями.

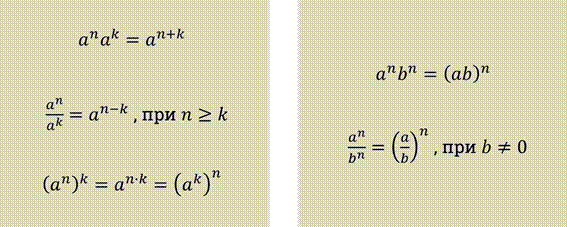
Вернёмся к нашему последнему одночлену и упростим его.

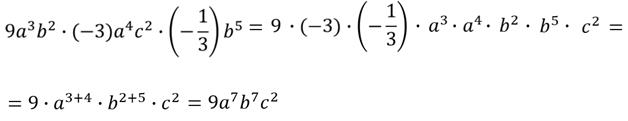
Получили одночлен: .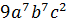

Такой вид одночлена называется стандартным.

Запомните, что в одночлене стандартного вида множители расположены в определённом порядке: на первом месте располагается числовой множитель, записанный цифрами, а за ним произведение степеней различных переменных.

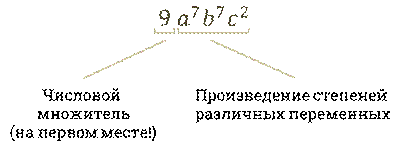
При этом следует знать, что буквы в одночленах стандартного вида принято записывать в алфавитном порядке.

Кстати, любой одночлен можно привести к стандартному виду. Вспомним алгоритм приведения одночлена к стандартному виду.

Для того чтобы одночлен привести к стандартному виду нужно:

1) перемножить все числовые множители;

2) поставить полученный числовой множитель на первое место;

3) перемножить все степени, то есть получить буквенную часть.

Пример.

Привести к стандартному виду одночлен: .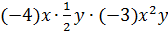

Решение: перемножим отдельно числовые множители и отдельно степени переменных. В результате получим,

Обратите внимание, что любое число представляет собой одночлен стандартного вида.

Задание.

Среди одночленов: 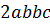 ;  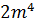 ;  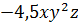 ;  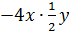 ;  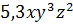 укажите одночлены стандартного вида.

Решение: первый одночлен хоть и представляет собой произведение, но заметим, что в нём дважды повторяется переменная b. А это говорит о том, что он не записан в стандартном виде.

Чего нельзя сказать о втором одночлене. Он является произведением числа и степени переменной. А значит, записан в стандартном виде.

Следующий одночлен представляет собой произведение числа и степеней переменных. Причём, все переменные записаны в алфавитном порядке. Следовательно, он записан в стандартном виде.

Четвёртый одночлен является произведением. Но заметим, числовой множитель не упрощён. Значит, данный одночлен не записан в стандартном виде.

И последний одночлен. Он представляет собой произведение числа и степеней переменных. Причём, все переменные записаны в алфавитном порядке. Следовательно, он записан в стандартном виде.

Определение.

Числовой множитель в одночлене стандартного вида называется коэффициентом одночлена.

В указанных нами одночленах стандартного вида коэффициенты равны 2, – 4,5 и 5,3.

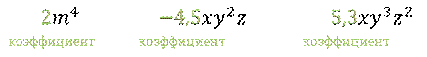
Если коэффициент равен 𝟏, то он не пишется. Например,

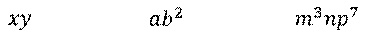
Если коэффициент равен (−𝟏), то пишется только знак «–» перед буквенными множителями. Например,

Вернёмся к одночлену 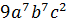. И давайте найдём сумму степеней всех переменных в рассматриваемом одночлене. Ее нетрудно посчитать. Она равна 16. Напомним, такую сумму называют степенью одночлена.

Определение.

Степенью одночлена называют сумму показателей степеней всех переменных, входящих в него.

Если одночлен является числом, отличным от нуля, то его степень считается равной нулю. Например, степень одночлена  равна нулю. Степень одночлена 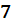 также равна нулю.

Можно также сказать, что это одночлены нулевой степени. А вот степень нулевого одночлена не определена.

Задание.

Найти степени одночленов:  ;   ;  .

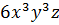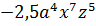Решение: степень первого одночлена 5𝑥𝑦 равна 2, так как степени переменных 𝑥 и 𝑦 равны единице.

Степень второго одночлена 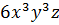 равна:

Третий одночлен: 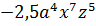 является одночленом 16-ой степени, так как

Определение.

Одночлены, приведённые к стандартному виду, называются подобными, если они имеют одинаковую буквенную часть.

Подобные одночлены можно:

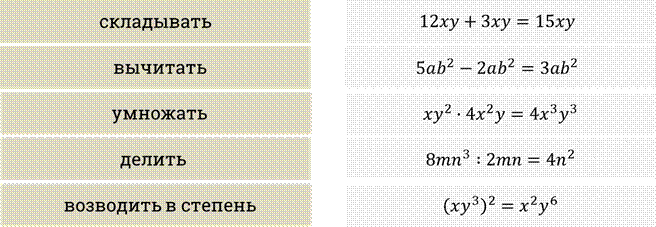
Сложение и вычитание подобных одночленов называется приведением подобных членов.

Перемножить или разделить два одночлена – это значит представить их произведение или частное в стандартном виде.

Возвести одночлен в степень – это значит представить эту степень в стандартном виде. 

Задание.

Выполнить действия:

а) найти сумму: 4𝑥,  6𝑥,  𝑥;                                          

б) найти разность: ,  ;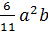                                            

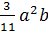в) найти произведение: , ;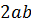

г) возвести во 2-ую степень: ;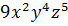

д) найти частное: , .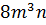

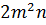Решение. В первом примере нужно найти сумму одночленов. Все эти три одночлена имеют стандартный вид и одинаковую буквенную часть. Следовательно, они подобны. И значит, можем найти их сумму. Для этого мы сложим их коэффициенты, а буквенную часть перепишем без изменений. Получим,

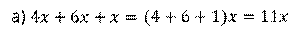
Таким образом, мы сложили три одночлена и в результате получили одночлен, который также представлен в стандартном виде.

Во втором примере нужно найти разность одночленов. Данные одночлены записаны в стандартном виде и подобны. Значит, можем найти их разность. Для этого мы вычтем коэффициенты, а буквенную часть перепишем без изменений. Получим,

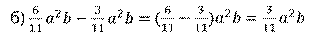
В следующем примере найдём произведение одночленов. Это одночлены стандартного вида, так как у них на первом месте располагаются числовые множители, а за ними следуют степени переменных. Запишем произведение этих одночленов. Далее воспользуемся переместительным и сочетательным свойствами умножения. Затем перемножим числовые множители и выполним умножение степеней с одинаковыми основаниями. В результате получим,

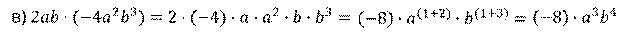
Таким образом, мы умножили один одночлен на другой и в результате получили одночлен, который представили в стандартном виде.

В следующем примере нужно возвести одночлен во вторую степень. Воспользуемся правилом возведения в степень произведения и получим,

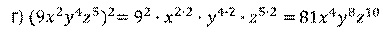
Таким образом, возведя одночлен в степень, мы также получили одночлен, причём стандартного вида.

И последний пример. Здесь нам нужно выполнить деление одночленов. Оба одночлена имеют стандартный вид. Для более удобного решения будем использовать черту дроби. Сначала разделим числовые коэффициенты. Затем разделим буквенные множители одночленов, опираясь на теорему о делении степеней. Получим,

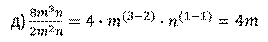
Таким образом мы разделили один одночлен на другой и в результате снова получили одночлен стандартного вида.

Напомним, что не всегда при делении одночленов результатом будет одночлен. В случае, если делитель содержит переменные, которые присутствуют в делимом, причём некоторые или все соответствующие показатели степеней в делителе больше, чем в делимом, то результатом такого деления будет алгебраическая дробь.

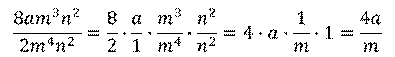
Также алгебраическую дробь мы получим и в случае, если делитель содержит переменные, которые отсутствуют в делимом.

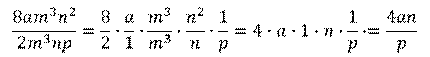
Итоги урока

На этом уроке мы повторили основные понятия, связанные с одночленами. А именно, вспомнили, что одночленом называется произведение чисел и степеней переменных с натуральными показателями. Кстати, числа и степени переменных также считаются одночленами. А вот число нуль называется нулевым одночленом. Вспомнили, как одночлены приводить к стандартному виду. Поговорили о их коэффициентах и степенях одночленов. Затем вспомнили какие одночлены являются подобными и выполнили действия над ними.