Вопросы занятия:
· вспомнить, что называют процентом;
· рассмотреть, как переводить дроби (десятичные и обыкновенные) в проценты и наоборот;
· рассмотреть основные типы задач на проценты и методы их решения.
Материал урока
С процентами каждый человек встречается, так или иначе, ежедневно: на работе, на учёбе, в магазине и так далее.

Само слово процент произошло от латинского слова «pro centum», что буквально означает «за сотню» или «со ста».
Долгое время под процентами понимались исключительно прибыль или убыток на каждые сто рублей. Они применялись только в торговых и денежных сделках. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчётах, статистике, науке и технике.
Определение.
В математике же, процент – это одна сотая часть любой величины или числа.
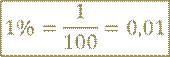
Слово «процент» после числа
заменяют знаком  .Знак
.Знак  происходит,
как полагают, от итальянского слова cento (сенто – сто), которое в
процентных расчётах часто писалось сокращенно cto. Отсюда путём
дальнейшего упрощения в скорописи буква t превратилась в наклонную
черту, возник современный символ для обозначения процента.
происходит,
как полагают, от итальянского слова cento (сенто – сто), которое в
процентных расчётах часто писалось сокращенно cto. Отсюда путём
дальнейшего упрощения в скорописи буква t превратилась в наклонную
черту, возник современный символ для обозначения процента.
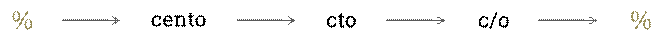
Проценты тесно связаны с обыкновенными и десятичными дробями. Очень важно уметь переводить дроби (десятичные и обыкновенные) в проценты и наоборот.
Правила.
Чтобы перевести десятичную дробь в проценты, нужно дробь умножить на 100 и добавить знак процента.
Пример.
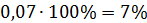
Чтобы перевести обыкновенную дробь в проценты, нужно сначала перевести её в десятичную дробь, а потом умножить на 100 и добавить знак процента.
Пример.
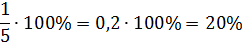
Чтобы проценты перевести в число, нужно убрать знак процента и разделить число на 100.
Пример.
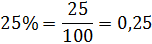
Задание.
Записать в процентах десятичные дроби:
а) 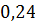 ; б)
; б)
 ; в)
; в)
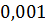 .
.
Решение: первая десятичная дробь 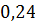 . Чтобы
перевести её в проценты, мы должны умножить данную дробь на 100 и добавить знак
процента. В результате получим,
. Чтобы
перевести её в проценты, мы должны умножить данную дробь на 100 и добавить знак
процента. В результате получим,
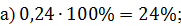
Переведём следующую дробь в проценты.
 умножим
на 100 и добавим знак процента. Получим,
умножим
на 100 и добавим знак процента. Получим,
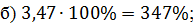
И осталась последняя десятичная
дробь. 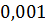 умножим
на 100 и добавим знак процента. В итоге получим,
умножим
на 100 и добавим знак процента. В итоге получим,
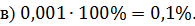
Задание.
Перевести обыкновенные дроби в проценты:
а)  ; б)
; б)
 ;
в)
;
в) 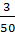 .
.
Решение: первая дробь  . Для
начала переведём её в десятичную. Помним, что обыкновенная дробь
. Для
начала переведём её в десятичную. Помним, что обыкновенная дробь  равна
десятичной дроби
равна
десятичной дроби 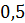 . Затем
мы должны эту десятичную дробь умножить на 100 и добавить знак процента. Получим,
. Затем
мы должны эту десятичную дробь умножить на 100 и добавить знак процента. Получим,
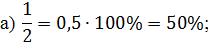
Следующая дробь  .
Переведём её в десятичную. Для этого разделим числитель на знаменатель.
Получим,
.
Переведём её в десятичную. Для этого разделим числитель на знаменатель.
Получим,  . Теперь
умножим, получившуюся десятичную дробь на 100 и не забудем добавить знак
процента. В результате получим,
. Теперь
умножим, получившуюся десятичную дробь на 100 и не забудем добавить знак
процента. В результате получим,
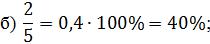
И последняя дробь в этом задании 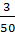 .
Переведём её в десятичную. То есть числитель разделим на знаменатель. Получим,
.
Переведём её в десятичную. То есть числитель разделим на знаменатель. Получим, 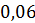 . А
дальше умножаем на 100 и добавляем знак процента. Получим,
. А
дальше умножаем на 100 и добавляем знак процента. Получим,
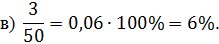
Задание.
Записать в виде десятичной дроби:
а) 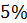 ; б)
; б)
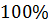 ;
в)
;
в) 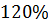 .
.
Решение: первыми записаны 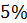 .
Разделим 5 на 100. Получим,
.
Разделим 5 на 100. Получим,
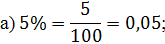
Следующими переведём в десятичную
дробь 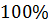 .
Разделим 100 на 100. Получим,
.
Разделим 100 на 100. Получим,
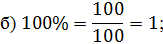
И переведём 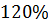 в десятичную дробь. Выполним деление. В результате получим,
в десятичную дробь. Выполним деление. В результате получим,
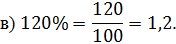
Теперь давайте разберёмся, как решать задачи на проценты.
Как правило, при решении задач на проценты некоторая величина 𝑎 принимается за 100%, а её часть – величина 𝑏 – принимается за 𝑥%. Затем составляют пропорцию:

Из этой пропорции определяют величину 𝑥, по правилу нахождения неизвестного члена пропорции по известным её трём членам.
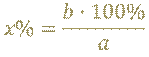
Рассмотрим наиболее распространённые типы задач на проценты и методы их решения.
Первый тип – это нахождение процента от числа.
Чтобы узнать, чему равны 𝑝% от некоторого числа 𝑎, нужно:

Или, чтобы найти данное число процентов от числа, нужно проценты записать десятичной дробью, а затем число умножить на эту десятичную дробь.
Задание.
Найти 3% от 180.
Решение:
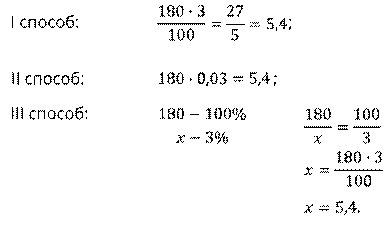
Каким способом решать, выбирать вам самим. Кому, как удобнее.
Задача. В магазин привезли 650 кг фруктов. Из них 28% составляют яблоки. Сколько килограмм яблок привезли в магазин?
Решение: напомним, чтобы найти число процентов от некоторого числа, нужно проценты записать десятичной дробью, а затем число умножить на эту десятичную дробь. По условию задачи, нам нужно найти 28% от 650.
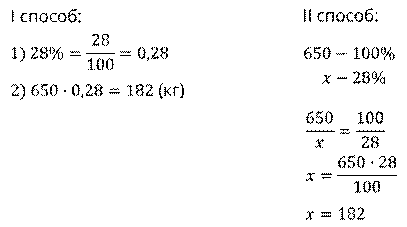
Ответ: 182 кг яблок привезли в магазин.
Обратим внимание, что при решении задач на проценты имеем прямо пропорциональную зависимость.
Второй тип задач: нахождение числа по его проценту.
Для того чтобы найти число 𝑎, если его 𝑝% равны 𝑏, надо:
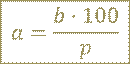
Или, чтобы найти число по данным его процентам, надо выразить проценты в виде дроби, а затем число разделить на эту дробь.
Задание.
Найти число, 3% которого равны 12.
Решение:
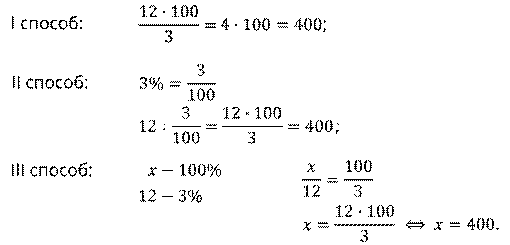
Задача. До конца урока осталось 9 минут. Известно, что это составляет 20% от всего урока. Сколько минут длится весь урок?
Решение: напомним, что для того чтобы найти число по данным его процентам, надо выразить проценты в виде дроби, а затем число разделить на эту дробь.

Следовательно, весь урок длится 45 минут.
Третий тип задач: нахождение процентного отношения двух чисел (часть от целого числа).
Для того чтобы выразить в процентах частное двух чисел 𝑎 и 𝑏, нужно:
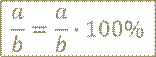
Задание.
Выразить число 8/5 в процентах.
Решение:

Задача. Вычислить, сколько процентов составляет 9 г соли в растворе массой 180 г.
Решение: напомним, что для того чтобы выразить в процентах частное двух чисел, нужно отношение этих чисел умножить на сто.
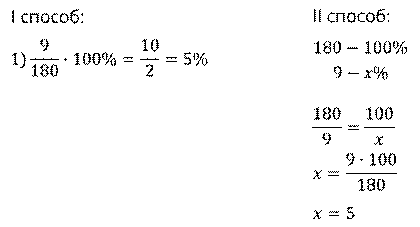
И четвёртый тип задач на проценты: вычисление процентного выражения одного числа от другого.
Чтобы найти, сколько процентов одно число 𝑎 составляет от другого 𝑏, нужно:
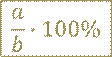
Задание.
Вычислить, сколько процентов составляет число 10 от числа 40.
Решение:

Задача. В палисаднике возле школы посадили 50 роз. Из них, 15 роз белого цвета. Сколько процентов от всех роз составляют белые розы?
Решение: напомним, что для того чтобы найти, сколько процентов одно число составляет от другого, нужно разделить первое число на второе и полученную дробь записать в виде процентов.
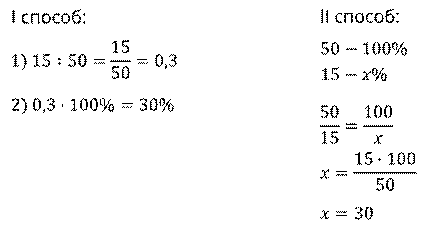
Следовательно, белые розы составляют 30 процентов от всех роз, посаженных в палисаднике.
Итоги урока
На этом уроке мы рассмотрели тему «проценты». Вспомнили, что называют процентом. Поговорили о том, как переводить дроби (десятичные и обыкновенные) в проценты и наоборот. Затем рассмотрели основные типы задач на проценты и методы их решения.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 4655
4655

