Получите свидетельство
Вход
«Я плохо представляю, что происходит с людьми:
они учатся не путем понимания. Они учатся
каким-то другим способом — путем механического
запоминания или как-то иначе. Их знания так хрупки!»
Ричард Фейнман
Данная тема будет посвящена рассмотрению основных формул, связанных с разделом динамики материальной точки, а также методических рекомендаций и порядок действий при решении задач на данную тему.
Динамика — это раздел механики, посвященный изучению движения тел под действием приложенных к ним сил.
Иными словами, в этом разделе будут рассматриваться причины появления у тел ускорений, то есть причины, которые вызывают изменение состояния движения тел. Основные положения динамики были сформулированы Исааком Ньютоном в 1687 году в виде трех законов, из которых как следствия получаются уравнения, необходимые для решения задач динамики. Важно помнить следующее: законы Ньютона относятся к материальной точке и телам, движущимся поступательно. Однако не забывайте и то, что далеко не всегда тело можно считать материальной точкой.
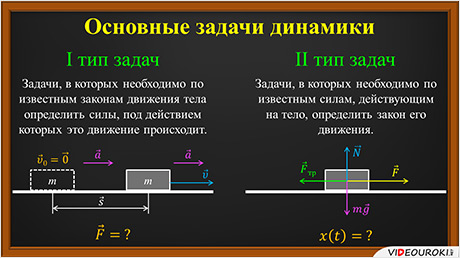
В динамике рассматриваются два типа задач. К первому типу относятся задачи, в которых необходимо по известным законам движения тела определить силы, под действием которых это движение происходит.
А ко второму — задачи, где надо по известным силам, действующим на тело, определить закон его движения, т. е. его положение, скорость и ускорение в любой момент времени. Задачи второго типа являются в динамике основными.
Законы динамики справедливы только при изучении движения по отношению к инерциальной системе отсчета. Инерциальные системы отсчёта – это такие системы отсчета, относительно которых материальная точка сохраняет состояние покоя или равномерного прямолинейного движения, если на него не действуют внешние силы, или действие этих сил скомпенсировано.
При этом считается, что течение времени во всех инерциальных системах отсчета происходит одинаково, то есть время носит абсолютный характер в механике Ньютона.
Скорость движения инерциальных систем отсчета не влияет на ускорение материальной точки и на силы взаимодействия между этими точками.
Масса данного тела в механике Ньютона не зависит от выбора инерциальной системы отсчета.
Таким образом, можно заключить, что во всех инерциальных системах отсчета механические процессы протекают одинаково и подчиняются одним и тем же законам. Эти утверждения выражают механический принцип относительности Галилея — Ньютона. Исходя из этого принципа, выбор инерциальной системы отсчета диктуется удобством решения динамической задачи, при этом следует помнить, что положение точки, ее скорость, траектория различны в разных инерциальных системах отсчета.
Три вида сил являются предметом рассмотрения в динамике материальной точки: силы упругости, силы трения и гравитационные силы.
Сила упругости возникает в результате деформации тел, т. е. при изменении их формы и размеров. Силу упругости, действующую со стороны опоры, называют силой нормальной реакции опоры, а действующую со стороны подвеса — силой натяжения подвеса.
Во многих задачах рассматриваются одномерные (линейные) деформации растяжения либо сжатия. В этих случаях силы упругости направлены вдоль осей продольно деформируемых нитей, стержней и определяются по закону Гука.
Силы трения — это силы, которые возникают при взаимодействии соприкасающихся тел и препятствуют их перемещению относительно друг друга. При сухом трении (то есть когда между соприкасающимися поверхностями отсутствует жидкая прослойка) различают три вида сил трения:
– сила трения покоя (она возникает при попытке вывести тело из состояния покоя и препятствует движению одного тела по поверхности другого);
– сила трения скольжения (она возникает при соприкосновении движущихся относительно друг друга тел и затрудняет их движение);
– сила трения качения (возникает, когда одно тело катится по поверхности другого тела).
Решая задачи, будем приближенно считать, что максимальное значение силы трения покоя равно силе трения скольжения.
Гравитационные силы, которые возникают при взаимном притяжении, присущем всем материальным объектам. К ним относят силу тяготения, силу тяжести (как одну из составляющих силы тяготения) и вес тела.
Напомним, что силу тяготения открыл Исаак Ньютон в одна тысяча шестьсот восемьдесят втором году, сформулировав свой закон всемирного тяготения, согласно которому, все тела во Вселенной притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.
Сила тяжести тела — это сила, с которой тело притягивается Землей.
А весом тела называют силу, с которой тело вследствие притяжения к Земле действует на горизонтальную опору или вертикальный подвес, удерживающие его от свободного падения
Сведём в таблицу основные формулы динамики материальной точки.
Основные формулы динамики материальной точки.
|
Формула |
Описание формулы |
|
|
Второй
закон Ньютона, где |
|
|
Третий
закон Ньютона, где |
|
|
Закон Гука, где Fx — проекция силы упругости, k — жесткость тела, х — абсолютное удлинение. |
|
|
Сила трения скольжения, где Fтр.п.max — максимальная сила трения покоя , μ — коэффициент трения, N — сила реакции опоры. |
|
|
Закон всемирного тяготения, где G = 6,67×10–11 (Н×м2)/кг2, F – сила притяжения, m1 и m2 — массы тел, которые притягиваются, r — расстояние между телами. |
|
|
Сила тяжести, где g — ускорение свободного падения. |
|
|
Ускорение свободного падения, вблизи поверхности небесного тела. |
|
|
Ускорение свободного падения на некоторой высоте от поверхности небесного тела. |
|
|
Вес тела. |
|
|
Линейная скорость спутника, движущегося по круговой орбите, где G — гравитационная постоянная, M — масса планеты, R — ее радиус, h — высота спутника над поверхностью планеты. |
|
|
Первая космическая скорость тела для планеты. |
–
результирующее ускорение тела, 
–
равнодействующая всех сил, действующих на тело, m
— масса тела.
и
–
силы взаимодействия двух тел.
Методические рекомендации по решению задач на динамику материальной точки.
1) Определить направление и характер движения тела.
2) сделать схематический чертеж, на котором тело изобразить в виде прямоугольника (или кружка) только в целях наглядности, а все силы, действующие на него, указать приложенными в одной точке, т. е. тело рассмотреть как материальную точку. Изображая силы, приложенные к телу, необходимо руководствоваться третьим законом Ньютона, помня, что силы могут действовать на тело только со стороны каких-то других тел.
3) записать второй закон Ньютона в виде
Первая запись второго закона Ньютона более приемлема с точки зрения физики, а со второй удобнее производить математические выкладки.
4) если рассматривается движение системы связанных между собой тел, то уравнения движения записывают для каждого тела в отдельности.
При этом следует помнить, что тела, связанные нерастяжимой нитью, имеют равные по модулю ускорения. Если нить перекинута через блок, причем массы нити и блока, а также силы трения, возникающие при вращении блока, достаточно малы, то натянутая нить действует с одинаковыми силами как на одно, так и на другое тело.
5) перейти от векторной формы записи уравнения динамики к скалярной, причем надо руководствоваться следующим правилом:
Если силы действуют вдоль нескольких прямых, но лежат в одной плоскости, надо выбрать две взаимно перпендикулярные оси Ох и Оу, лежащие в плоскости действия сил. Тело изобразить в произвольной точке траектории, а оси координат (заметим, не оси системы отсчета) связать с этим телом. Спроектировав все векторы, входящие в основное уравнение динамики, на эти оси и записать его в виде двух скалярных уравнений.
Если движение прямолинейное, то одну из осей следует направить вдоль вектора ускорения, а другую — ей перпендикулярно.
6) если в задаче требуется найти не только силы и ускорения, но также координаты тел и их скорости, то дополнительно следует написать кинематические уравнения, связывающие их в выбранной системе отсчета. Решить полученную систему уравнений относительно неизвестных величин. Решение получить в общем виде и проверить правило размерностей. Получить результат в численном виде в единицах СИ и оценить его реальность.
0
9115
