Вы замечали, что предметы обихода (например, раковина умывальника, ванна, края газовой плиты, садовый инвентарь, детские игрушки и прочее) не имеют острых углов? Углы в них скруглены. Как вы думаете, для чего?
Во-первых, в целях безопасности — для предотвращения травм. Во-вторых, для увеличения прочности конструкции. А в-третьих, для улучшения внешнего вида изделий.
Если присмотреться, то можно заметить, что контуры большинства предметов и объектов окружающего нас мира состоят из сочетаний различных линий (прямых, дуг, окружностей), пересекающихся между собой и плавно переходящих одна в другую.
Так вот, такие скругления углов, то есть плавные переходы одной поверхности в другую, одной линии в другую, называются сопряжением.
Все сопряжения на чертежах выполняют дугами окружностей заданных размеров. Чтобы построить сопряжение, необходимы следующие элементы: радиус сопряжения, центр сопряжения и точки сопряжения.

Центр сопряжения — это точка, из которой проводят дугу плавного перехода одной линии к другой.
Радиус сопряжения — это радиус дуги сопряжения, с помощью которой происходит сопряжение.
Точка сопряжения — это общая точка сопрягаемых линий. В точках сопряжений происходит плавный переход (касание) линий.
Посмотрите на этот рисунок и подумайте, на каком расстоянии от контура детали расположены центры сопряжения. Верно, на одинаковом. А чему же равно это расстояние?

Всё верно, равно радиусу сопряжения. А теперь подумайте, как получены точки сопряжения? Посмотрите внимательно на рисунок. Точки сопряжения — это точки пересечения перпендикуляров, опущенных из центра сопряжения на сопрягаемые прямые, с этими прямыми.
Вот мы и установили ключевые моменты построения сопряжения.
Итак, первое что мы делаем, это находим центр сопряжения, который должен располагаться на одинаковом расстоянии от сопрягаемых прямых. Затем мы строим точки сопряжения как результат пересечения перпендикуляра, опущенного из центра сопряжения, с сопрягаемыми прямыми. И, наконец, проводим сопрягающую дугу.
Обычно задания на сопряжения содержат графическое условие: сопрягаемые элементы (например, две пересекающиеся прямые) и радиус сопряжения. Чтобы не допустить ошибки в построении сопряжения, его выполняют по алгоритму.
Рассмотрим построение сопряжений различных типов. И начнём мы с простого — алгоритма построения сопряжения острого угла или двух прямых, пересекающихся подострым углом, дугой заданного радиуса.
Итак, в начале мы должны построить центр сопряжения.
Для этого из произвольных точек К и К1 восстановим перпендикуляры к сопрягаемым прямым АВ и АС. Далее на перпендикулярах от точек К и К1 отложим величину заданного радиуса сопряжения (для этого можно воспользоваться циркулем). И, наконец, через точки, отмеченные на перпендикулярах, проводим прямые, параллельные прямым АВ и АС, до их взаимного пересечения. Полученная точка — точка О — и есть центр сопряжения.

Теперь нам нужно построить точки сопряжения.
Для этого мы просто опускаем из точки О перпендикуляры на сопрягаемые прямые АВ и АС, воспользовавшись, например, угольником. В итоге получаем две точки сопряжения.
Чтобы выполнить сопряжение, мы должны заданным радиусом сопряжения из центра О провести дугу сопряжения между точками 1 и 2. В конце мы с вами должны выполнить обводку чертежа в следующем порядке.
Вначале мы с помощью кругового циркуля обводим сопрягающую дугу основной сплошной толстой линией (напомним, что её толщина должна быть равна 1 миллиметру).
Затем обводят основной сплошной толстой линией (карандашом твёрдости ТМ или М) сопрягаемые прямые, начиная от точек 1 и 2.
Теперь давайте с вами разберём алгоритм построения сопряжения дугой заданного радиуса прямых, пересекающихся под тупым и прямым углами. Проводить построения мы будем одновременно.
Как и в прошлый раз, начинаем мы с построения центра сопряжения.
Для этого из произвольных точек восстанавливаем перпендикуляры к сопрягаемым прямым. Далее на этих перпендикулярах откладываем величину заданного радиуса сопряжения. И, наконец, через точки, отмеченные на перпендикулярах, проводим прямые, параллельные заданным прямым, до их взаимного пересечения. Полученная точка — точка и есть центр сопряжения.

Теперь строим точки сопряжения.
Для этого мы опускаем из центра сопряжения перпендикуляры на сопрягаемые прямые. В итоге получаем по две точки сопряжения для каждого из случаев.
Далее мы строим сопрягающие дуги заданного радиуса. Для этого мы заданным радиусом сопряжения из центра сопряжения проводим дуги сопряжения между точками 1 и 2. Вот и всё. Нам осталось только выполнить обводку чертежа.
Теперь предположим, что нам нужно построить сопряжения двух параллельных прямых. Посмотрим, как это сделать.
Итак, для начала выберем на одной из прямой произвольную точку, например, точку С. В этой точке восстанавливаем перпендикуляр до пересечения его со второй прямой, например, в точке D.
Теперь, чтобы найти центр сопряжения, мы с вами должны разделить полученный отрезок DC пополам. Напомним, как это делается. Итак, из точек D и С радиусом, который больше половины длины отрезка, проводим дуги до их взаимного пересечения. Полученные точки пересечения соединяем прямой, которая является перпендикуляром к отрезку DC. Точка пересечения О делит наш отрезок на две равные части.

Далее, из найденного центра сопряжения радиусом сопряжения, равным R = OD = ОС проводим дугу, соединяя точки сопряжения D и С. В конце производим обводку чертежа.
На очереди у нас с вами построение сопряжения прямой и окружности.
Первое, что нужно сделать при таком построении, это провести вспомогательную прямую, параллельную данной прямой и удалённую от неё на расстоянии, равным радиусу сопряжения (R1).
Затем из центра окружности О проведём вспомогательную дугу радиусом, равным сумме радиусов окружности R и дуги сопряжения R1, до её пересечения с вспомогательной прямой. Получаем центр сопряжения. Из полученной точки опускаем перпендикуляр до его пересечения с заданной прямой в точке В — это будет наша первая точка сопряжения.

Чтобы найти вторую точку сопряжения, мы с вами должны соединить центр окружности (точку О) с центром сопряжения (точкой О1). Теперь из центра сопряжения радиусом сопряжения R1 проводим дугу сопряжения, соединив точки сопряжения А и В.
Алгоритм выполнения сопряжения окружности и прямой линии по внешнему контуру практически не отличается от только что нами рассмотренного. Главное отличие состоит в том, что радиус вспомогательной дуги должен быть равен разности радиусов дуги сопряжения R1 и окружности R.

Теперь давайте посмотрим, как выполняется построение касательной к окружности из заданной точки.
Итак, в начале соединим заданную точку А с центром окружности О. Далее нам с вами необходимо разделить полученный отрезок ОА пополам.
Теперь из точки О, радиусом R равным О1А построим вспомогательную окружность. Точка пересечения вспомогательной окружности и заданной окружности и является точкой сопряжения.

Соединив точку сопряжения с точкой, заданной по условию, получим искомую касательную к окружности.
Построить касательную к окружности можно и без использования дуг, а с помощью угольника и линейки.

Очень часто требуется построить сопряжения двух окружностей. Сопряжение двух окружностей осуществляется по внутреннему и внешнему контурам или может быть смешанным.
Для начала рассмотрим пример сопряжения двух окружностей с радиусами R1 и R2 дугой радиусом R по внешнему контуру.
Итак, проведём из центра окружностей вспомогательные дуги радиусом, равным сумме радиусов окружностей (R + R1 и R + R2) до их пересечения. Тем самым мы с вами нашли центр сопряжения.

Далее точку пересечения вспомогательных дуг соединяем с центрами заданных окружностей. Полученные точки пересечения — это точки сопряжения. Соединив точки сопряжения дугой сопряжения радиусом сопряжения, получим искомое сопряжение двух окружностей по внешнему контуру.
Что касается построения сопряжения двух окружностей по внутреннему контуру, то оно схоже с построением сопряжения по внешнему контуру. Разница состоит лишь в том, что из центров окружностей проводят вспомогательные дуги радиусом, равным разности радиусов окружностей (R – R1 и R – R2).

Попробуйте самостоятельно установить алгоритм построения смешанного сопряжения, используя наш рисунок-подсказку

В заключение отметим, что сегодня сложно представить, что когда-то люди рисовали, чертили и создавали шедевры без помощи графических редакторов и программ для моделирования. Именно поэтому работы современного художника из Венесуэлы Рафаэля Араужо кажутся особенно интересными.

Мастер без помощи компьютера и современных технологий создаёт чертежи и расчёты полёта бабочек или раковины моллюска с помощью циркуля, лекала, линейки и карандаша, используя геометрические построения на основе принципа золотого сечения.

 Получите свидетельство
Получите свидетельство Вход
Вход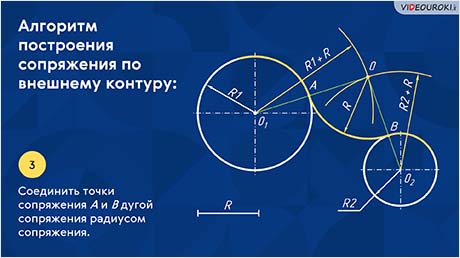




 1910
1910

