Деление отрезка, угла и окружности на равные части

При разработке графических документов выполняют различные геометрические построения, например делят отрезок или угол на равное количество частей, строят перпендикуляр к прямой линии, сопряжения и тому подобное.

Многие из этих построений вам уже знакомы из уроков математики или других предметов. При этом вы использовали транспортир, угольники, линейки с делениями и калькулятор для расчётов. Особенность геометрических построений в черчении заключается в том, что при этом можно обойтись без математических расчётов. Всё подчиняется определённым алгоритмам, каждый из которых представляет собой совокупность графических операций, выполняемых в строгой последовательности.

Для начала, давайте познакомимся с алгоритмом деления отрезка на две и четыре равные части при помощи циркуля.

Итак, для начала из концов отрезка АВ одним и тем же радиусом больше половины длины отрезка нужно провести дуги до их взаимного пересечения.

Далее эти точки пересечения соединяют прямой, которая является перпендикуляром к данному отрезку АВ. Точка пересечения С делит заданный отрезок на две равные части.

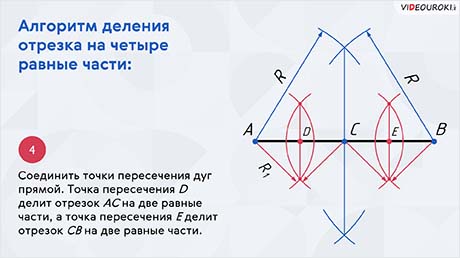
Аналогично делят отрезок на четыре равные части. Вообще же, так можно разделить отрезок прямой на любое количество равных частей, кратное двум.

Теперь давайте посмотрим, можно как разделить отрезок на n равных частей.

Итак, из точки А под произвольным острым углом к заданному отрезку АВ проводят вспомогательный луч АС.

Далее на прямой АС откладывают равные отрезки произвольной величины (то количество отрезков, на которое необходимо разделить отрезок АВ), например на 5.

Последнюю точку n соединяют с точкой В и получают линию nB.

Теперь из каждой точки луча АС проводят прямые, параллельные отрезку nВ, которые и делят данный отрезок на заданное число равных частей.

Чтобы отложить равное количество отрезков на вспомогательной прямой можно воспользоваться циркулем (с неизменным раствором). А при проведении параллельных прямых, соединяющих отрезки Аn и АВ, воспользуйтесь линейкой и треугольником.

Теперь рассмотрим последовательность построения перпендикуляра из точки, лежащей вне прямой линии.

Конечно, тут самый простой способ — это воспользоваться угольником (как вы делали это на уроках математики). Но представим, что угольника у нас нет. Но есть циркуль.

Тогда нам необходимо из точки А (лежащей вне прямой), как из центра, произвольным радиусом описать дугу так, чтобы она пересекла прямую в двух точках В и С. Затем из точек В и С, как из центров, одинаковыми радиусами описываем дуги, чтобы они пересеклись в некоторой точке D.

Соединяем точку пересечения дуги D с точкой А и получаем искомый перпендикуляр.

Теперь представим, что нам нужно построить перпендикуляр из точки, лежащей на прямой линии без использования угольника.

Для этого мы с вами из заданной точки А (лежащей на прямой), как из центра, одинаковым радиусом описываем дуги так, чтобы они пересекали прямую в двух точках В и С.

Далее из точек В и С, как из центров, одинаковыми радиусами описываем дуги, чтобы они пересеклись в точке D.

Соединяя точку пересечения дуг D с точкой А получаем искомый перпендикуляр.

Теперь поговорим о построении углов. Самый простой способ построения углов — воспользоваться транспортиром. Давайте вспомним, как это делается.

Итак, пусть нам необходимо построить угол КОР, равный 57°. В начале с помощью линейки или ровного края транспортира мы начертим луч ОК, который является одной из сторон нашего угла. Затем наложим транспортир так, чтобы вершина угла О совпала с центром транспортира, а сторона ОК проходила через отметку 0 на верхней шкале. Отметим на верхней шкале транспортира возле отметки 57 точку Р. Теперь с помощью линейки или ровного края транспортира проводим луч ОР. Вот и всё — заданный угол построен.

Некоторые углы можно построить и с помощью двух треугольников и линейки.

Здесь важно помнить, что мы пользуемся прямоугольными треугольниками с известными углами — 30°, 60° и 90° и 45°, 45° и 90°. Поэтому построение этих углов не должно вызывать трудностей.

Теперь, если вспомнить, что внешний угол треугольника равен разности между 180° и его внутренним углом, смежным с ним, то можно построить углы в 120°, 150° и 135°.

А использование различных комбинаций треугольников и линейки, можно построить и некоторые другие углы.

Кстати, углы 30°, 45°, 60° и 90° градусов легко строятся по клеточкам в тетради.

Если по каким-либо причинам у вас нет угольников, то можно воспользоваться циркулем. Рассмотрим последовательность построения угла 60° градусов.

Итак, из точки О произвольным радиусом R проводят дугу до её пересечения с прямой в точке А.

Из точки А этим же радиусом R проводят вторую дугу так, чтобы она пересекла первую дугу в точке В.

Затем соединяют точки В и О и получают угол 60°.

Используя нашу подсказку, попробуйте самостоятельно установить алгоритм построение угла в 120°.

Часто бывает необходимым разделить заданный угол на две равные части (то есть найти его биссектрису). Это довольно легко сделать, имея под рукой только циркуль и линейку.

Для этого из вершины угла А произвольным радиусом проводят дугу до пересечения со сторонами угла ВАС. Получают две точки, например n и ).

Из полученных точек проводят дуги радиусом R, несколько большим половины длины дуги nk, до взаимного пересечения в точке m.

Вершину угла А соединяют с точкой m прямой, которая делит угол ВАС на две равные части.

Выполняя чертежи некоторых деталей, приходится делить окружность 3, 6, 8 и так далее равных частей, строить правильные многоугольники. Как же это делается?

Для начала посмотрим, как разделить окружность на две и четыре равные части.

Итак, любой диаметр делит окружность на две равные части А два взаимно перпендикулярных диаметра делят её на четыре равные части.

Если же соединить эти точки деления, то мы получим квадрат, вписанный в данную окружность.

А как вписать в окружность квадрат, стороны которого параллельны осевым линиям? Верно, следует разделить дуги между центровыми линиями пополам, то есть провести биссектрисы прямых углов.

Для этого нужно провести окружность с заданным радиусом R.

Из точек С и В тем же радиусом R, что и радиус окружности, провести дуги до их взаимного пересечения. Точку пересечения соединить прямой с центром окружности. Получаем две точки 1 и 3. Аналогично выполняют построение из точек А и С, пока не получат точки 2 и 4.

Соединяя последовательно найденные точки, получаем искомый квадрат, вписанный в окружность, у которого стороны параллельны центровым линиям. При этом наша окружность разделилась на четыре равные части.

А теперь посмотрите, если мы последовательно соединим все наши точки на окружности, то мы получим правильный восьмиугольник, вписанный в окружность. А сама окружность при этом окажется разделённой на восемь равных частей.

Теперь давайте рассмотрим алгоритм деления окружности на три равные части.

Итак, из точки А диаметра (А-1 проводим дугу радиусом заданной окружности до пересечения с окружностью в точках 2 и 3.

Соединив точки 1, 2 и 3, получаем вписанный правильный треугольник, вершины которого делят окружность на три равные части.

Аналогично можно вписать в окружность правильный треугольник, вершина которого — это произвольная точка окружности.

Чтобы разделить окружность на шесть равных частей, следует провести делящие дуги из противоположных концов одного из диаметров.

Обратите внимание: если провести делящие дуги из концов горизонтального диаметра, то получим вписанный правильный шестиугольник, у которого две вершины совпадают с концами горизонтально расположенной центровой линии.

Если же делящие дуги провести из концов вертикального диаметра, то получим вписанный правильный шестиугольник, у которого две вершины совпадают с концами вертикально расположенной центровой линии. Но в обоих случаях вершины шестиугольника делят окружность на шесть равных частей.

А как вы думаете, как можно разделить окружность на двенадцать равных частей и построить правильный двенадцатиугольник?...

Правильно, нужно соединить два способа деления окружности на шесть равных частей в одном построении.

Теперь давайте рассмотрим алгоритм деления окружности на пять равных частей.

Итак, из точки А радиусом окружности R проводят дугу до пересечения окружности в точках n и m. И соединяют полученные точки прямой линией. На пересечении с горизонтальной осевой линией получают точку В, которая является серединой отрезка ОА, то есть радиуса окружности.

Из точки В радиусом, равным отрезку ВС, проводят дугу, которая пересечёт горизонтальную осевую линию в точке D. Соединив точки С и D, получаем отрезок СD, который и является длиной стороны пятиугольника.

Теперь из точки С проводим дугу радиусом, равным СD, и получаем точки 5 и 2. Из полученных точек проводим ещё по одной дуге тем же радиусом (R = CD) и находим точки 3 и 4. Соединив полученные точки деления последовательно (1-2-3-4-5), получаем правильный вписанный пятиугольник.

А если соединить эти точки через одну (1-3-5-2-4-1), то мы получим пятиконечную звезду.

Для построения объёмной пятиконечной звезды выполняют следующие действия:

Проводят две окружности разного диаметра.

Далее делят большую окружность на пять равных частей.

После соединяют точки деления с центром окружностей и продолжают до пересечения с меньшей окружностью.

Затем поочерёдно соединяют точки, лежащие на большей и меньшей окружностях, и получают изображение звезды. Чтобы передать объём, можно затемнить части её лучей.

С помощью деления окружности на равные части составляются круговые орнаменты — узоры, украшающие различные сооружения, утварь, оружие и так далее. Основа создания орнамента — это геометрические построения. На рисунок орнамента могут влиять технические, растительные, текстовые мотивы. Круговые орнаменты могут быть как простыми, например для геометрической резьбы, так и очень сложными, требующими серьёзных геометрических построений.