Представим себе такую историю…
– Саша, что случилось? – спросил у друга Паша.
– Да вот задумался я немного, – ответил Саша. – Смотри, в школе уроки у нас длятся по 45 минут.
– Ну да! – согласился Паша. – И что тут странного?
– Да ничего странного, – улыбнулся Саша. – Просто мне стало интересно, а какую часть часа занимает 1 урок?
–
Так это же легко посчитать, – сказал Паша. – В 1 часе 60 минут, урок длится 45
минут. Тогда 45 минут от 1 часа составляют  .
.
–
То есть 1 урок занимает  часа? – задумался
Саша. — Такая большущая дробь получилась.
часа? – задумался
Саша. — Такая большущая дробь получилась.
–
Ну, можно уменьшить эту дробь, – продолжил Паша. – Мы можем числитель и
знаменатель нашей дроби разделить на 5. Получим дробь  . Кстати, и эту
дробь можно ещё уменьшить, – заметил Паша. — Числитель и знаменатель последней
дроби
. Кстати, и эту
дробь можно ещё уменьшить, – заметил Паша. — Числитель и знаменатель последней
дроби  делятся на 3. Разделим
эти числа. Получим дробь
делятся на 3. Разделим
эти числа. Получим дробь  .
.
–
Значит, 1 урок занимает  часа? – решил
уточнить Саша.
часа? – решил
уточнить Саша.

– Всё правильно! – ответил Паша.
– А как это ты сейчас так всё посчитал? – спросил Саша. – Что это за способ такой?
– Я сейчас занимался сокращением дробей, – ответил Паша.
– Сокращением? – задумался Саша. – А что это за сокращение такое?
– А давай лучше спросим у Мудряша, – предложил Паша. – Он точно сможет всё объяснить.
– Ребята, прежде чем я вас познакомлю с сокращением дробей, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.

– Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было получиться!
– Ну а теперь вернёмся к вашему вопросу, – начал Мудряш. — Но прежде давайте вспомним основное свойство дроби.
–
Если числитель и знаменатель дроби умножить на одно и то же натуральное число,
то получится равная ей дробь: 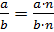 ,
, 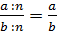 , – сказали
мальчишки.
, – сказали
мальчишки.
–
Молодцы! – похвалил ребят Мудряш. – Также вы знаете, что если числитель и
знаменатель дроби разделить на их общий делитель, то получится равная ей дробь.
– – – Когда вы искали, какую часть составляет урок длительностью 45 минут от
часа, то вы получили дробь  . Потом вы разделили
числитель и знаменатель этой дроби на 5 и получили равную ей дробь
. Потом вы разделили
числитель и знаменатель этой дроби на 5 и получили равную ей дробь  . В таком случае
говорят, что дробь
. В таком случае
говорят, что дробь  сократили на 5.
Но потом Паша заметил, что дробь
сократили на 5.
Но потом Паша заметил, что дробь  можно ещё
сократить на 3 и получили дробь
можно ещё
сократить на 3 и получили дробь  . В таком случае
говорят, что дробь
. В таком случае
говорят, что дробь  сократили на 3.
сократили на 3.

– Запомните! – сказал Мудряш. – Деление числителя и знаменателя на их общий делитель, отличный от одного, называют сокращением дроби. При сокращении дробь заменяют равной дробью с меньшим числителем и меньшим знаменателем. Поэтому сокращение дробей облегчает вычисления.
–
А почему мы остановились на дроби  и
не стали дальше сокращать её? – спросил Саша.
и
не стали дальше сокращать её? – спросил Саша.
–
Не всякую дробь можно сократить, – ответил Мудряш. – Дробь  сократить нельзя,
поскольку её числитель и знаменатель не имеют общих делителей, отличных от
единицы, то есть являются взаимно простыми числами. В таком случае говорят, что
дробь
сократить нельзя,
поскольку её числитель и знаменатель не имеют общих делителей, отличных от
единицы, то есть являются взаимно простыми числами. В таком случае говорят, что
дробь  – несократимая
дробь.
– несократимая
дробь.

– Запомните! – продолжил Мудряш. – Дробь, числитель и знаменатель которой – взаимно простые числа, называют несократимой. Если дробь можно сократить, то её обычно сокращают на наибольший общий делитель числителя и знаменателя. После такого сокращения общих делителей уже не остаётся, поэтому получается несократимая дробь.
–
Вот и с вашей дробью  можно было также
поступить, – продолжил Мудряш. – Вы дробь
можно было также
поступить, – продолжил Мудряш. – Вы дробь  сократили на 5,
получили дробь
сократили на 5,
получили дробь  , то есть
, то есть  равно
равно  . В свою очередь,
дробь
. В свою очередь,
дробь  вы
сократили на 3. Сократив дробь
вы
сократили на 3. Сократив дробь  на 3, вы получили
дробь
на 3, вы получили
дробь  , которая уже
является несократимой.
, которая уже
является несократимой.
– Да! – согласились мальчишки. – Мы всё так и делали.
–
Однако если дробь  сократить на 5
умножить на 3 равно 15, то несократимую дробь
сократить на 5
умножить на 3 равно 15, то несократимую дробь  можно
было получить сразу:
можно
было получить сразу: 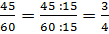 . Обратите
внимание, нам удалось сразу получить несократимую дробь, поскольку число 15 –
это есть наибольший общий делитель 45 и 60.
. Обратите
внимание, нам удалось сразу получить несократимую дробь, поскольку число 15 –
это есть наибольший общий делитель 45 и 60.

– Запомните! – сказал Мудряш. – Если сократить дробь на наибольший общий делитель числителя и знаменателя, то получится несократимая дробь.
–
Давайте сократим дробь 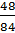 , – предложил
Мудряш.
, – предложил
Мудряш.
–
Для начала найдём наибольший общий делитель числителя и знаменателя этой дроби,
– сказал Паша. — Число 48 можно разложить на следующие простые множители: 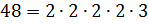 . А разложение на
простые множители числа 84 имеет такой вид:
. А разложение на
простые множители числа 84 имеет такой вид: 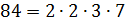 . Выпишем общие
множители наших чисел. Тогда наибольший общий делитель числителя и знаменателя
нашей дроби равен 12.
. Выпишем общие
множители наших чисел. Тогда наибольший общий делитель числителя и знаменателя
нашей дроби равен 12.
–
Осталось сократить дробь, – продолжил Саша. – Разделим числитель и знаменатель
дроби 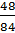 на 12. Получим
дробь
на 12. Получим
дробь  . Числа 4 и 7
взаимно простые. Значит, дробь
. Числа 4 и 7
взаимно простые. Значит, дробь  – несократимая.
– несократимая.

– Молодцы! – похвалил ребят Мудряш. А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.
Задание
первое: сократите дроби: а) 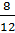 ; б)
; б) 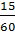 ; в)
; в) 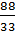 ; г)
; г)  ; д)
; д) 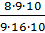 .
.
Решение:
первая дробь — 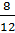 . Наибольший общий
делитель числителя и знаменателя этой дроби равен 4. Значит, можем сократить
дробь на 4. Получим дробь
. Наибольший общий
делитель числителя и знаменателя этой дроби равен 4. Значит, можем сократить
дробь на 4. Получим дробь  . Следующая дробь —
. Следующая дробь —
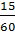 . Наибольший общий
делитель числителя и знаменателя этой дроби равен 15. Сократим дробь на 15.
Получим дробь
. Наибольший общий
делитель числителя и знаменателя этой дроби равен 15. Сократим дробь на 15.
Получим дробь  .
.
Следующая
дробь 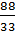 . Здесь наибольший
общий делитель числителя и знаменателя равен 11. Сократим. Получим дробь
. Здесь наибольший
общий делитель числителя и знаменателя равен 11. Сократим. Получим дробь  .
.
Перейдём
к следующей дроби  . В числителе
дроби записано произведение 3 и 4, а в знаменателе – произведение 5 и 8. Можем
сократить дробь на 4. Получим дробь
. В числителе
дроби записано произведение 3 и 4, а в знаменателе – произведение 5 и 8. Можем
сократить дробь на 4. Получим дробь 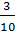 .
.
И
перейдём к последней дроби 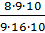 . Здесь снова
числитель и знаменатель дроби представлены в виде произведений чисел. Можем
сократить дробь на 8, затем сократим на 9 и потом сократим на 10. В результате
получим дробь
. Здесь снова
числитель и знаменатель дроби представлены в виде произведений чисел. Можем
сократить дробь на 8, затем сократим на 9 и потом сократим на 10. В результате
получим дробь  .
.

Следующее
задание: представьте десятичные дроби в виде обыкновенной
несократимой дроби: а) 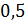 ; б)
; б)  ; в)
; в) 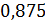 .
.
Решение: первая
десятичная дробь 0,5. Представим её в виде обыкновенной дроби 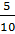 . Затем сократим
на 5 и получим дробь
. Затем сократим
на 5 и получим дробь  .
.
Следующая
дробь 0,75. Представим её в виде обыкновенной дроби 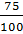 . Сократим на 25.
Получим дробь
. Сократим на 25.
Получим дробь  .
.
И
последняя десятичная дробь — 0,875. Представим её в виде обыкновенной дроби 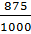 . Сократим дробь
сначала на 5. Получим дробь
. Сократим дробь
сначала на 5. Получим дробь 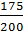 . Затем сократим
дробь ещё на 5. Получим дробь
. Затем сократим
дробь ещё на 5. Получим дробь  . И сократим дробь
ещё на 5. В результате получим дробь
. И сократим дробь
ещё на 5. В результате получим дробь  .
.


 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 2560
2560

