Равномерное движение точки по окружности

Вы уже знаете, что прямолинейное движение, тем более равномерное, встречается гораздо реже, нежели движение по криволинейной траектории. Кто из вас не наблюдал, как вращается волчок? А кто не катался на каруселях? Наконец, всем вам известно, что спутники обращаются вокруг планет почти по круговым траекториям, а планеты — вокруг центрального тела нашей Солнечной системы.

Криволинейных траекторий существует бесчисленное множество. Но оказывается, что любую кривую мы можем представить в виде совокупностей дуг окружностей разных радиусов и прямолинейных участков. Поэтому чаще всего изучение криволинейного движения сводится к изучению движения точки по окружности.

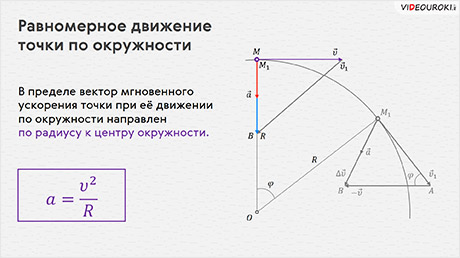
Мы будем изучать самый простой вид такого движения — равномерное движение точки по окружности. При таком движении направления векторов скорости и ускорения непрерывно изменяются, но вот их модули остаются постоянным.

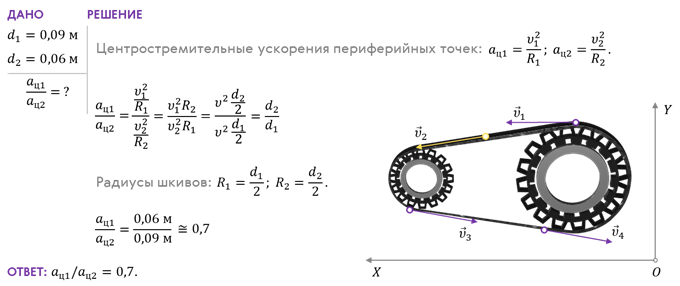
Итак, пусть материальная точка, равномерно движущаяся по окружности радиуса R, в некоторый момент времени t занимает положение М и имеет скорость υ, а спустя некоторый промежуток времени — положением М₁ и скорость υ₁. Найдём модуль и направление вектора ускорения точки в положении М.

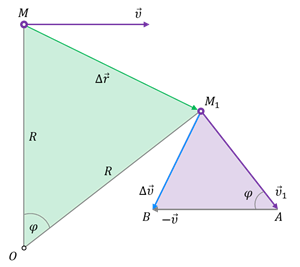
Давайте найдём вектор изменения скорости за исследуемый промежуток времени:

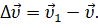
Теперь давайте посмотрим на два треугольника ОММ₁ и М₁АВ. Что можно о них сказать? Во-первых, очевидно, что это два равнобедренных треугольника, так как ОМ и ОМ₁ — это радиусы окружности, а длины векторов скорости (их модули) одинаковы, так как движение точки у нас равномерное. Наконец, угол 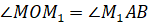 как углы между двумя взаимно перпендикулярными сторонами. Следовательно, эти два треугольника подобны. Поэтому мы можем записать, что модуль изменения скорости точки так относится к модулю её скорости, как модуль перемещения к радиусу окружности, по которой эта точка движется:

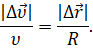
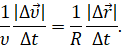
Как мы уже с вами знаем, отношение модуля изменения скорости к промежутку времени, в течении которого это изменение произошло, — это модуль среднего ускорения точки. А отношение модуля перемещения к этому промежутку времени — это модуль средней скорости перемещения:

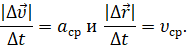
Теперь давайте с вами вспомним, что при стремлении промежутка времени к нулю отношение изменения скорости к промежутку времени, в течение которого это изменение произошло, называется ускорением. А отношение перемещения к промежутку времени называется мгновенной скоростью. Эти определения справедливы и для модулей скорости и ускорения:

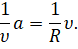
После простых преобразований получим, что модуль ускорения точки при её движении по окружности прямо пропорционален квадрату модуля её скорости и обратно пропорционален радиусу окружности:

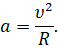
Учитывая, что при равномерном движении точки по окружности модуль её скорости и радиус окружности не меняются с течением времени, то и модуль вектора ускорения всё время остаётся неизменным. Но вот его направление, как и направление вектора скорости, меняется от точки к точке.

Найдём направление вектора ускорения.  Мы уже знаем, что в общем случае вектор ускорения направлен так же, как и вектор изменения скорости точки при стремлении промежутка времени к нулю. Но тогда точка М₁ будет бесконечно близко подходить к точке М, а угол φ будет стремиться к нулю. А вот угол  будет стремиться к 90^о. Значит, угол между вектором изменения скорости точки и радиусом окружности стремится к нулю при стремлении к нулю промежутка времени. Учитывая, что направление вектора ускорения совпадает с направлением вектора изменения скорости, получим, что в пределе вектор мгновенного ускорения направлен по радиусу к центру окружности. Поэтому ускорение точки при её движении по окружности и называют центростремительным или нормальным, так как оно направлено по нормали к вектору мгновенной скорости.

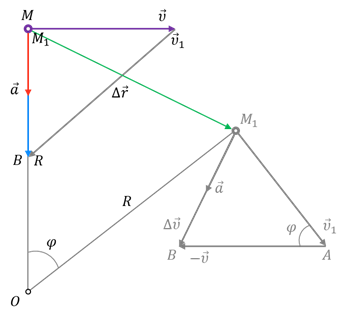
Задача 1. В ремённой передаче диаметр ведущего шкива равен 6 см, а ведомого — 9 см. Сравните центростремительные ускорения периферийных точек каждого шкива.

Задача 2. Два тела движутся по окружности радиусом 36 м в одном направлении с постоянными по модулю скоростями. Нормальное ускорение первого тела равно 10 м/с², а второго — 4 м/с². Через какой минимальный промежуток времени тела окажутся в одной точке траектории?

В заключение отметим, что равномерное движение точки по окружности является движением с переменной скоростью и переменным ускорением, так как направление их векторов непрерывно изменяется. Но их модули при этом остаются неизменными.