Для упорядочивания больших массивов данных используют таблицы. С их помощью можно быстро найти нужную информацию. Однако таблицы не дают наглядного представления о соотношении величин. Чтобы наглядно представить соотношение данных между собой, используют диаграммы. Диаграммы часто встречаются в газетах, журналах, книгах для иллюстрации различных данных.
Столбиковая диаграмма, которая наглядно отражает данные о количестве проданных блокнотов, приведённые в таблице. Высоты столбиков диаграммы наглядно отражают соотношение между величинами.

Глядя на эту диаграмму, можно сказать, что больше всего блокнотов было продано в понедельник, а меньше всего – в субботу. Также можно отметить, что в конце недели продаётся меньше блокнотов, чем в начале.
Давайте поговорим о круговых диаграммах.
Рассмотрим пример. 5 подружек решили вскладчину купить торт, который стоит 360 р. Вика внесла 100 р., Ира – 80 р., Катя – 90 р., Лиза – 40 р., Оля – 50 р.
Схема в виде круга, которая показывает долю каждой девочки.

Так как торт стоит 360 р., то каждому рублю соответствует сектор круга с углом 1º.
Сектор круга – это часть круга, которая ограничена дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Отметим, что если бы девочки делили торт не поровну, а пропорционально своим долям в общей сумме, то Вике достался бы сектор торта с углом 100º, Ире – сектор с углом 80º, Кате – сектор с углом 90º, Лизе – сектор с углом 40º, Оле – сектор с углом 50º.
Деление круга на секторы позволяет наглядно показать доли целого в самых различных случаях. Этот способ довольно прост и убедителен. Полученная таким способом схема деления называется круговой диаграммой.
Круговая диаграмма – это диаграмма, которая показывает, как целое делится на части в виде секторов круга, углы которых пропорциональны долям единого целого.
Чтобы построить круговую диаграмму на бумаге, нужны линейка, циркуль и транспортир.
Напомним, что циркуль – это инструмент для черчения окружностей и дуг, а транспортир – это инструмент для построения и измерения углов.
Чтобы раскрасить секторы, полезно иметь цветные карандаши или фломастеры.
Следует отметить, что нет необходимости строить углы очень точно. Например, посмотрите на две круговые диаграммы. На первой диаграмме малый сектор имеет угол ровно 60º, а на второй – ровно 61º. При рассмотрении данных диаграмм эти различия не видны.

При построении круговой диаграммы не нужно откладывать углы с большой точностью. Так как небольшая погрешность не мешает правильно воспринимать диаграмму.
Главными достоинствами круговой диаграммы являются наглядность восприятия и быстрота построения.
Для точного представления и анализа данных диаграммы не подходят. Для этого нужны таблицы.
Так как целое делится на несколько частей, то диаграмма состоит из нескольких секторов. Угол каждого сектора приближённо пропорционален той доле, которую он показывает.
Иногда встречаются неудачные диаграммы. Например, на этой диаграмме показано деление целого на 2 части. Но проще было бы сказать, что четверть избирателей не явилась на участок для голосования.

На следующей круговой диаграмме все 4 доли примерно одинаковы. Лучше было бы написать: «Все 4 вида шоколада (горький, молочный, белый и рубиновый) пользуются примерно одинаковым спросом».

Пример. В таблице даны сведения о площади всех материков Земли.

Давайте построим круговую диаграмму, показывающую долю каждого материка в общей площади поверхности всех материков Земли.
Сначала найдём общую площадь поверхности всех материков. Для этого запишем сумму всех площадей и выполним сложение.

Теперь найдём долю каждого материка и угол соответствующего сектора. При необходимости для удобства вычисления будем округлять найденные значения до тысячных. Результаты вычислений будем заносить в таблицу.
Доля Евразии примерно равна 0,367. Следовательно, сектор, соответствующий Евразии, имеет угол, равный 321,12º.
Доля Африки примерно равна 0,203. Следовательно, сектор, соответствующий этому материку, имеет угол, равный 73,08º.
Доля Северной Америки примерно равна 0,164. А значит, сектор, соответствующий этому материку, имеет угол, равный 59,04º.
Доля Южной Америки примерно равна 0,119. Значит, сектор, соответствующий Южной Америке, имеет угол, равный 42,84º.
Доля Антарктиды примерно равна 0,095. Следовательно, сектор, соответствующий этому материку, имеет угол, равный 34,2º.
Доля Австралии примерно равна 0,052. А значит, сектор, соответствующий Австралии, имеет угол, равный 18,72º.

При построении диаграммы можно округлить углы до целого числа градусов или даже до углов, кратных 5º.
Раскрасим секторы разными цветами и добавим легенду, которая упростит чтение и понимание диаграммы.

Теперь наглядно видно, что Евразия занимает меньше половины площади, а Африка – чуть меньше четверти.
Столбиковые диаграммы удобны, когда нужно показать, как одна и та же величина меняется со временем, или когда нужно сравнить разные (но сравнимые) величины. А вот круговая диаграмма нужна для других целей. Она показывает, как целое делится на части.
До встречи на следующих занятиях!

 Получите свидетельство
Получите свидетельство Вход
Вход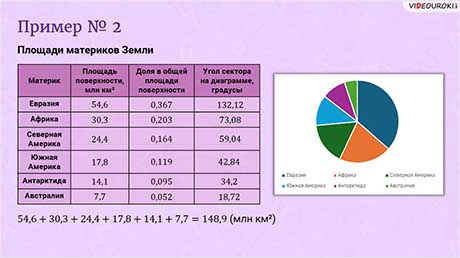




 2553
2553


