Среднее арифметическое числового массива

Перед вами таблица, в которой приведены данные о производстве кукурузы в России с 2016 года по 2020 год.

Рассматривая данные за каждый год отдельно, мы не можем получить полное представления об уровне производства кукурузы в стране. Ведь, как видно из таблицы, производство в разные годы различается. Оно зависит от погодных условий, площади посева и других обстоятельств.

Чтобы получить полное представление об уровне производства кукурузы в стране, нужно использовать среднее значение за ряд лет.

По данным таблицы мы можем вычислить среднее значение производства кукурузы за 5 лет. Для этого сложим годовые сборы кукурузы, а затем разделим сумму на количество слагаемых, то есть на 5.

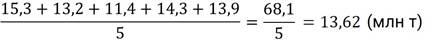
Для простоты можно считать, что массив состоит не из значений производства, которые измеряются в миллионах тонн, а из чисел. Поэтому мы не писали единицы измерения у каждого слагаемого, а указали их один раз в конце в скобках.

Получается, что среднее производство кукурузы в России за рассматриваемый период составило тринадцать целых шестьдесят две сотых миллионов тонн в год.

Найденное значение называется средним арифметическим.

Средним арифметическим числового массива называется отношение суммы всех чисел массива к их количеству.

Другими словами, среднее арифметическое – это дробь, в числителе которой стоит сумма чисел, а в знаменателе – их количество.

Иногда среднее арифметическое называют просто средним, или средним значением.

Давайте снова вернёмся к таблице с данными о производстве кукурузы в России и на числовую ось точками нанесём все величины, среднее значение укажем стрелкой.

Видим, что два числа меньше среднего и три больше. При этом обратите внимание, что значения 13,2 и 13,9 довольно близки к среднему.

Среднее значение является центром набора чисел. Поясним, что в данном случае означает слово «центр».

Представьте, что числовая ось является стержнем, на который в точках, соответствующих отмеченным числам, подвешены одинаковые гири.

На стержне существует точка равновесия, на которую можно «опереть» стержень с гирями так, что стержень окажется в равновесии. Этой точкой оказывается среднее арифметическое. В физике точку равновесия называют центром масс.

Рассмотренный пример с гирями иллюстрирует главное свойство среднего арифметического. Среднее арифметическое одинаково зависит от всех чисел набора. И большие, и малые числа входят в среднее арифметическое «с одинаковым весом».

Однако в некоторых случаях это достоинство оборачивается недостатком: если в наборе по ошибке или в силу каких-то особенных причин есть очень большое или очень малое значение, то оно одно очень сильно влияет на среднее арифметическое. Тогда среднее не очень хорошо описывает весь остальной набор в целом.

Среднее арифметическое хорошо описывает однородные массивы данных, то есть массивы, в которых величины имеют один и тот же смысл, и нет значений, которые сильно отличаются от большинства.

А теперь давайте выполним несколько заданий.

Задание первое. Найдите среднее арифметическое чисел:

Решение.

Напомним, что средним арифметическим числового массива называется отношение суммы всех чисел массива к их количеству.

Задание второе. Сколько из данных чисел меньше среднего значения, а сколько больше среднего значения?

Решение.

Задание третье. Вычислите среднее арифметическое наборов чисел. Какую закономерность можно наблюдать в поведении средних значений в пунктах б) и в) по сравнению со средним значением в пункте а)?

Решение. Прежде чем вычислить среднее арифметическое данных наборов чисел, обратим внимание на то, что числовые наборы б) и в) получены из набора чисел а) умножением всех чисел на 2 и на 4 соответственно.

Посмотрим на найденные средние значения и заметим, что среднее значение числового набора б) в 2 раза больше среднего значения числового набора а), среднее значение числового набора в) в 4 раза больше среднего значения числового набора а).

Можно сделать вывод, что средние значения наборов б) и в) получены из среднего значения набора а) умножением на 2 и на 4 соответственно.

Задание четвёртое. В таблице приведена урожайность зерновых культур в России с 1992 года по 2001 год.

Найдите среднюю урожайность зерновых культур в России за разные периоды времени.

Решение. Найдём среднюю урожайность зерновых культур в России за 5 лет: с т1992 года по 1996 год.

Найдём среднюю урожайность зерновых культур в России за 5 лет: с 1997 года по 2001 год.

Осталось найти среднюю урожайность зерновых культур в России за весь период: с 1992 года по 2001 год.

Обратите внимание, что найденные средние значения не сильно различаются между собой.

До встречи на следующих занятиях!