Ранее мы говорили, что механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени. Вспомним с вами, что движение тела может быть прямолинейным, то есть когда траекторией движения является прямая линия. А может быть и криволинейным, когда траекторией движения является кривая линия.
Самым простым видом криволинейного движения является движение тела по окружности. Вообще, такой вид движения довольно часто встречается в повседневной жизни. Взять хотя бы движение планет вокруг своей оси или вокруг Солнца. Кроме этого, существуют ещё сотни примеров: вращение колеса автомобиля, движение стрелок часов и многое-многое другое. Иными словами, криволинейных траекторий существует бесчисленное множество. Но оказывается, что любую кривую мы можем представить в виде совокупностей дуг окружностей разных радиусов и прямолинейных участков. Поэтому чаще всего изучение криволинейного движения сводится к изучению движения точки по окружности.
Мы будем изучать самый простой вид такого движения — равномерное движение тела по окружности. Равномерным движением по окружности называется такое движение, при котором материальная точка за любые равные промежутки времени описывает одинаковые дуги (иногда говорят, что тело поворачивается на одинаковые углы за одинаковые промежутки времени).
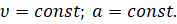
Итак, пусть материальная точка, равномерно движущаяся по окружности радиуса R, в некоторый момент времени t занимает положение М и имеет скорость υ, а спустя некоторый промежуток времени — положением М1 и скорость υ1. Найдём модуль и направление вектора ускорения точки в положении М.

Но для начала давайте найдём вектор изменения скорости за исследуемый промежуток времени:

Теперь
давайте посмотрим на два вырисовавшихся треугольника ОММ1 и М1АВ.
Что можно о них сказать? Правильно, во-первых это два равнобедренных
треугольника, так как ОМ и ОМ1 — это радиусы
окружности, а длины векторов υ и υ1 одинаковы, так как
движение точки у нас равномерное. Наконец, угол  как
углы между двумя взаимно перпендикулярными сторонами (по свойству касательной и
построению). Следовательно, эти два треугольника подобны. Поэтому мы можем
записать, что модуль изменения скорости точки так относится к модулю её
скорости, как модуль перемещения к радиусу окружности, по которой эта точка
движется:
как
углы между двумя взаимно перпендикулярными сторонами (по свойству касательной и
построению). Следовательно, эти два треугольника подобны. Поэтому мы можем
записать, что модуль изменения скорости точки так относится к модулю её
скорости, как модуль перемещения к радиусу окружности, по которой эта точка
движется:

Теперь разделим записанное равенство на промежуток времени, в течение которого точка перешла из положения М в положение М1:

Как мы уже с вами знаем, отношение модуля изменения скорости к промежутку времени, в течение которого это изменение произошло, — это модуль среднего ускорения точки. А отношение модуля перемещения к этому промежутку времени — это модуль средней скорости перемещения:

Теперь давайте с вами вспомним, что при стремлении промежутка времени к нулю отношение изменения скорости к промежутку времени, в течение которого это изменение произошло, называется ускорением. А отношение перемещения к промежутку времени называется мгновенной скоростью. Эти определения справедливы и для модулей скорости и ускорения:

После простых преобразований получим, что модуль ускорения точки при её движении по окружности прямо пропорционален квадрату модуля её скорости и обратно пропорционален радиусу окружности:

Учитывая, что при равномерном движении точки по окружности модуль её скорости и радиус окружности не меняются с течением времени, то и модуль вектора ускорения всё время остаётся неизменным. Но вот его направление, как и направление вектора скорости, меняется от точки к точке. Найдём это направление.
Мы
уже знаем, что в общем случае вектор ускорения направлен так же, как и вектор
изменения скорости. Но тогда точка М1 будет бесконечно близко
подходить к точке М. Угол φ будет стремиться к нулю. А вот угол  будет
стремиться к 90о. Значит, угол между вектором изменения скорости
точки и радиусом окружности стремится к нулю при стремлении к нулю промежутка
времени. Учитывая, что направление вектора ускорения совпадает с направлением
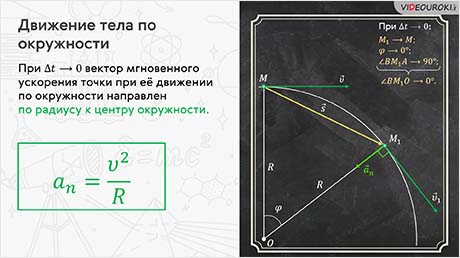
вектора изменения скорости, получим, что в пределе вектор мгновенного ускорения
направлен по радиусу к центру окружности. Поэтому ускорение точки при её
движении по окружности и называют центростремительным или нормальным, так
как оно направлено по нормали к вектору мгновенной скорости.
будет
стремиться к 90о. Значит, угол между вектором изменения скорости
точки и радиусом окружности стремится к нулю при стремлении к нулю промежутка
времени. Учитывая, что направление вектора ускорения совпадает с направлением
вектора изменения скорости, получим, что в пределе вектор мгновенного ускорения
направлен по радиусу к центру окружности. Поэтому ускорение точки при её
движении по окружности и называют центростремительным или нормальным, так
как оно направлено по нормали к вектору мгновенной скорости.

Вспомним ещё несколько важных физических величин, описывающих криволинейное движение. В первую очередь, это, конечно же, период обращения. Периодом обращения называется промежуток времени, за который тело совершает один полный оборот по окружности:

Единицей измерения периода в системе СИ, является секунда.
Существует также величина, обратная периоду, которая называется частотой. Эта величина равна числу оборотов в единицу времени:

Очевидно, что период обращения и частота обратно пропорциональны. Основная единица измерения частоты — это герц, хотя часто можно встретить и секунду в минус первой степени.

Ещё одной важной характеристикой движения по окружности является угловая скорость. Под угловой скоростью точки, равномерно движущейся по окружности, понимают отношение угла поворота радиуса, проведённого к точке, к промежутку времени, в течение которого совершён этот поворот:


Измеряется угловая скорость в радианах на секунду:

Мы знаем, что Δ𝑡 = 𝑇; Δ𝜑 = 2𝜋.
Тогда, угловая скорость будет равна

Также, мы знаем, что длина окружности 𝑙 = 2𝜋𝑅. Поэтому, линейная скорость тела, при его движении по окружности, будет определяться отношением длины окружности к периоду обращения:

А теперь сравним две формулы для определения линейной и угловой скорости. Как видно из записей линейная скорость равна произведению угловой скорости и радиуса окружности:

Это вполне логично: чем дальше точка находится от центра, вокруг которого она вращается, тем больше должна быть её линейная скорость, чтобы за одинаковое время совершить поворот на одинаковый угол.
Но вернёмся к центростремительному ускорению и получим ещё одну формулу для его определения с учётом выражения, связывающей линейную и угловую скорость обращения. Тогда, центростремительное ускорение можно найти, как произведение квадрата угловой скорости и радиуса окружности, по которой движется тело:

В заключение отметим, что равномерное движение точки по окружности является движением с переменной скоростью и переменным ускорением, так как направление их векторов непрерывно изменяется. Но их модули при этом остаются неизменными.

 Получите свидетельство
Получите свидетельство Вход
Вход




 1315
1315

