Мы часто вместо слова «масса» говорим «вес», а слова «массивный» и «тяжёлый» считаем синонимами. Однако с точки зрения физики — это грубая ошибка. Представим, что на Луне установлена обитаемая космическая станция. Находясь на ней, любой учащийся вашего класса смог бы поднять стокилограммовую гирю! Меньше ли на Луне вес гири? Да. Меньше ли на Луне масса гири? Нет.
Так что такое масса? Каковы её свойства?
Для начала давайте проведём с вами несколько простых опытов со стальным шариком, подвешенным на нити, прикреплённой к неподвижному штативу. Сначала на шарик покоится, так как сила упругости нити компенсирует притяжение Земли. Если же мы к шарику поднесём сбоку магнит, то под его действием шарик начнёт двигаться.

Уберём магнит, а нить, на которой висит шарик, перережем. Шарик упал. Причём упал он ускоренно, так как воздействие Земли было не уравновешено.
Такие вот простые опыты и другие многочисленные наблюдения за различными телами в окружающем мире позволяют сделать вывод, что ускоренное движение тела есть результат нескомпенсированного воздействия на него других тел.
Чтобы исследовать, как происходит взаимодействие тел и от чего зависят их ускорения при этом, вспомним простой классический эксперимент. Возьмём два одинаковых по размеру цилиндра из алюминия и меди, скреплённых нитью и находящихся на гладком стержне, вдоль которого они могут легко скользить. Стержень с цилиндрами закреплён в установке, которая может вращаться с постоянной угловой скоростью в горизонтальной плоскости.

Так как цилиндры взаимодействуют друг с другом с помощью нити, то при вращении стержня, они будут вращаться вместе с ним, находясь на определённых расстояниях от оси вращения. Зафиксируем эти расстояния.
А теперь давайте попробуем сравнить центростремительные ускорения наших цилиндров. И так, предположим, что цилиндры вращались с некоторой постоянной угловой скоростью ω. Тогда мы можем записать, что центростремительные ускорения цилиндров равны произведению угловой скорости и радиусов окружностей, по которым вращались цилиндры:
a1 = ωR1; a2 = ωR2.
Далее сравним модули ускорений цилиндров, разделив почленно первое уравнение на второе:
![]()
Мы приходим к тому, что модули ускорений цилиндров относятся как радиусы окружностей, по которым вращаются их центры. Последние мы с вами легко можем определить при помощи линейки или мерной ленты.
Подставив найденные радиусы в наше уравнение, получаем, что искомое отношение примерно равно 3,3.
Если мы повторим этот опыт при другой угловой скорости вращения или связав цилиндры нитью другой длины, то радиусы окружностей изменятся. Но вот их отношение, а значит, и отношение модулей ускорений останется тем же.
Давайте вспомним, как объясняется это постоянство отношений. И так, мы знаем, что ускорение характеризует быстроту изменения скорости тела. А в седьмом классе вы познакомились с физической величиной — массой тела, от которой также зависела величина изменения скорости тела. Вы знаете, что, чем больше масса тела, тем труднее изменить его скорость. Или, как говорят в физике, чем больше масса, тем более инертно тело. (Напомним, что инертность — это свойство тел приобретать определённое ускорение при данном взаимодействии).
Давайте сравним массы медного и алюминиевого цилиндров. Так как их размеры одинаковы, то одинаковы и их объёмы. При этом масса тела связана с его объёмом формулой m = ρV, где ρ — это плотность вещества, из которого изготовлено тело.
Здесь мы с вами немного отвлечёмся и вспомним, что плотностью вещества называют массу этого вещества, содержащегося в единице его объёма:
![]()
Например, когда говорят, что плотность вещества равна 900 кг/м3, то имеется в виду, что 1 м3 этого вещества имеет массу 900 кг.

Также напомним, что наибольшую плотность имеют вещества, находящиеся в твёрдом состоянии. А наименьшую — газы. Исключением из этого правила является вода, плотность которой в твёрдом состоянии меньше, чем в жидком.
Но вернёмся к нашим расчётам и найдём отношение масс медного и алюминиевого цилиндров:

После небольших преобразований найдём, что искомое отношение масс цилиндров равно отношению их плотностей. Если подставить в найденное отношение значения плотностей меди и алюминия, то получим примерно 3,3.
Сравнение отношений модулей ускорений и масс цилиндров показывает, что ускорения цилиндров обратно пропорциональны их массам:
![]()
Многочисленные эксперименты по исследованию самых разнообразных взаимодействий тел показывают, что данная закономерность выполняется всегда.
Таким образом, отношение модулей ускорений двух взаимодействующих тел равно обратному отношению их масс:
![]()
Таким образом масса характеризует меру инертности тел. Поэтому её ещё называют инертной массой.
Но массу тела можно определить и по силе притяжения тел друг к другу. Такую массу в физике называют гравитационной.
Неоднократные опыты и современные эксперименты гарантируют, что различие инертной и гравитационной масс (если оно есть) для тела массой в одну тонну меньше одной миллионной грамма. Иными словами, считают, что гравитационная и инертная массы равны: 𝑚гр=𝑚ин.
Масса тела обладает свойством аддитивности, то есть масса тела равна сумме масс всех частиц (или материальных точек), из которых оно состоит:
![]()
Также, для данной системы тел выполняется закон сохранения массы, который впервые был сформулированный русским учёным Михаилом Васильевичем Ломоносовым в 1748 году — при любых процессах, происходящих в системе, её масса остаётся неизменной.
Эти два свойства массы кажутся очевидными. Однако они выполняются лишь приближённо. Дело в том, что если два или несколько тел объединяются в одно с выделением энергии, то масса объединённого тела будет меньше, чем сумма масс исходных тел! Так происходит потому, что масса является мерой энергии, заключённой в теле. Такой вывод был сделан Альбертом Эйнштейном ещё в 1905 году. (Оказывается, в одном грамме любого вещества запасено столько энергии, сколько её выделяется при сгорании 20 000 тонн нефти!)

То, что одна физическая величина — масса — характеризует самые важные свойства материи (инертные, гравитационные и энергетические) — один из самых важных законов природы.
Вы конечно же знаете, что единицей массы в СИ является килограмм (кг). Это масса специально изготовленного эталона, который хранится в Международном бюро мер и весов, расположенного в Севре близ Парижа. Он представляет собой цилиндр диаметром и высотой 39,17 мм, изготовленного из сплава платины и иридия.

С помощью эталона массы можно определить массу тела путём взвешивания на весах. Существуют различные типы весов: рычажные, пружинные, электронные. Во всех случаях весы — это прибор для определения массы тела по действующей на него силе тяжести. Как вы знаете, сила тяжести прямо пропорциональна массе тела:
F = gm.

Рычажные весы с равными плечами находятся в равновесии, если силы тяжести взвешиваемого тела и набора гирь равны:
gmтела = gmгирь, то есть при mтела = mгирь.
Значит, результат взвешивания на рычажных весах не зависит от значения коэффициента g и будет одним и тем же на любой планете.
Также если привести во взаимодействие эталон и тело неизвестной массы, а затем измерить их ускорения, то можно определить неизвестную массу тела, как произведение отношения ускорения эталона к ускорению тела и массы эталона:
![]()
Конечно, для обычных тел такой способ менее удобен, чем привычное нам взвешивание. Зато определение масс космических тел, например планет по ускорению их спутников или мельчайших частиц вещества по ускорению при их взаимодействии, производится практически всегда.

 Получите свидетельство
Получите свидетельство Вход
Вход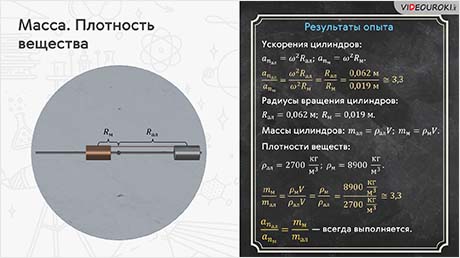




 1371
1371

