Плоскость. Прямая. Луч

Давайте представим себе такую историю.

В математике она

Пригождается всегда:

Без хвоста от запятой

Всем нам кажется простой.

И в конце, закончив строчку,

Мы поставим, братцы…

– Ну это легкотня! Это же точка! – обрадовался Саша.

– Саша, а что ты делаешь? – спросил Паша.

– Нам по математике задали разгадать загадки.

– А можно я с тобой вместе поразгадываю? – спросил Паша.

– Конечно! – обрадовался Саша, – вместе же интереснее. И ребята принялись читать загадки.

Линию прямую, ну-ка,

Сам нарисовать сумей-ка!

Это сложная наука!

Пригодится здесь...

– Линейка! – обрадовался Паша. Давай следующую загадку.

Он ограничен с двух сторон

И по линейке проведён.

Длину его измерить можно,

И сделать это так несложно!

– Я знаю, что это! – обрадовался Саша, – это отрезок! Помнишь, нам Электроша о нём рассказывал? Давай читать следующую загадку.

Он от солнца прилетает,

Пробивая толщу туч,

И в тетрадочке бывает,

А зовётся просто…

– Эта загадка уже посложнее, – задумался Саша.

– Смотри! – воскликнул Паша, – если внимательно читать эту загадку, то там в начале говорится, что он прилетает от солнца сквозь толщу туч. Мне кажется, я догадался… это же луч!

– Точно! – обрадовался Саша, – но в загадке говорится, что он бывает и в тетрадке. Как луч может оказаться в тетрадке?

– Не знаю, – задумался Паша, – но точно знаю, кто может нам помочь!

– Ребята, прежде чем я вас познакомлю с ещё несколькими геометрическими фигурами, хочу, чтобы вы немного размялись и выполнили устные задания, – предложил Электроша.

 – Давайте сверимся! – сказал Электроша. – Посмотрите, что у вас должно было получиться!

– Ну а теперь самое время познакомить вас с такими геометрическими фигурами, как луч и прямая, – начал Электроша, – но сначала вам нужно усвоить ещё кое-какое понятие. Мы с вами уже научились строить отрезки в тетради. Но скажите, на сколько большой отрезок вы сможете построить в своей тетради? – спросил он у ребят.

– Самый большой отрезок в тетради получится, если чертить его, начиная с одного угла листа и заканчивая в противоположном ему углу, – предположил Паша.

– Да, – согласился Электроша. Как видите, размеры тетради ограничивают нас и не дают нам строить отрезки очень большой длины. А давайте попробуем представить себе, что тетрадный лист с помощью волшебного заклинания вырос до размеров поверхности стола. Длина вашего большого отрезка как-то поменялась?

– Да! – воскликнули мальчишки, – он стал ещё больше!

– А теперь представьте себе, что этот тетрадный лист стал ещё больше, например, размером с футбольное поле. Что стало с длиной вашего отрезка? – спросил ребят Электроша.

– Он стал огромным! – представляли отрезок мальчишки.

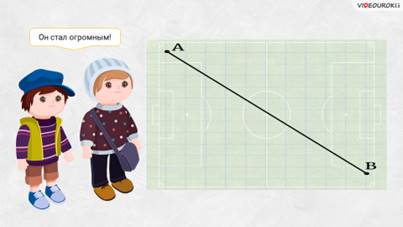
Поверхности тетрадного листа, стола, футбольного поля дают нам представление о плоскости, – продолжил Электроша. Только эти поверхности имеют границы, а плоскость в математике безгранична во всех направлениях.

Запомните! Плоскость бесконечна. Поэтому эту геометрическую фигуру нельзя изобразить, но её можно вообразить.

– А значит, на плоскости можно начертить отрезок очень большой длины? – решил спросить Паша.

– И не только, – ответил Электроша. Вот давайте построим отрезок АВ. Напоминаю, что отрезок – это кратчайшая линия, соединяющая две точки.

Если этот отрезок с помощью линейки продлить в обе стороны, то мы получим ещё одну геометрическую фигуру, которую называют прямой.

– А где прямая заканчивается? – спросил Саша.

– Ребята, запомните! – сказал Электроша, – прямая не имеет концов. Она бесконечна. Поэтому на рисунке мы можем изобразить только часть прямой, но мысленно мы должны понимать, что прямая продолжается в обе стороны бесконечно.

– А теперь давайте отметим на листе бумаги две точки – А и В. Проведём через них прямую. А теперь попробуйте через эти же две точки провести ещё одну прямую. Получается?

– Нет, – задумались мальчишки.

– Запомните! – сказал Электроша. – Через любые две точки проходит одна единственная прямая.

Это свойство позволяет обозначать прямую, называя две любые её точки. Так, например, прямую, которую мы с вами сейчас построили, обозначают одним из двух способов: АВ или ВА. А читают: «прямая АВ» или «прямая ВА». Точки А и В лежат на прямой.

Но иногда прямые обозначают одной строчной латинской буквой. Посмотрите, на листе я построил две прямые: прямую m и прямую n.

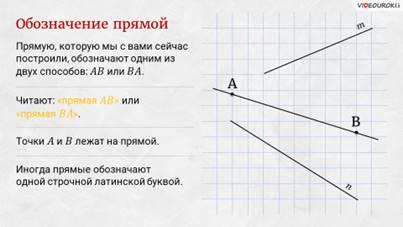
Любая прямая делит плоскость на две части, на две полуплоскости.

– Электроша, а что это за фигура, которая называется лучом? – решили спросить мальчишки, вспомнив о своей загадке.

– Сейчас я вам объясню, – сказал Электроша.

Давайте построим прямую АВ и отметим на ней точку О. Посмотрите, эта точка разделила нашу прямую на две части. Каждую их этих частей называют лучом с началом в точке О. Конца у луча нет.

– То есть луч имеет начало, но не имеет конца? – спросил Паша.

– Правильно! – ответил Электроша. – Геометрический луч очень похож на световой, поэтому его так и назвали. Чтобы лучше представить себе луч, вспомним лазерную указку. Вспомнили? Луч света начинается в лазерной указке и уходит в бесконечность по прямой.

– Теперь понятно, – сказал Паша.

– А как обозначают лучи в математике? – спросил Саша.

– Так же, как и прямую, – ответил Электроша. – Луч обозначают двумя прописными буквами, только сначала записывают букву, которая обозначает начало луча, а потом букву, обозначающую какую-либо другую точку этого луча. Так, в нашем примере, точка О делит прямую АВ на два луча: луч ОА и луч ОВ. Переставлять буквы в названии луча нельзя. Первой буквой всегда обозначается начало луча. Лучи, на которые точка разбивает прямую, называют дополнительными друг другу.

И, кстати, луч – это ещё один пример геометрической фигуры.

– Запомните, ребята, в отличие от прямой, луч бесконечен только в одну сторону.

– Электроша, я совсем запутался, – перебил Электрошу Саша, – отрезок, прямая, луч – они такие все одинаковые, чертятся прямой линией, обозначаются буквами…

– Сейчас я вам покажу, чем они отличаются, и вы быстренько их запомните, – сказал Электроша. – Отрезок, луч, прямая являются прямыми линиями. А различаются они наличием концов. Запомните! У отрезка два конца, у луча – один, а у прямой нет ни одного.

– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.

Задание первое: назовите фигуры, изображённые на рисунке.

Решение: на рисунке изображены отрезки АВ, АК и КВ; лучи АК, ВА, КА, КВ; прямая АВ.

Следующее задание. Ответить на вопрос: пересекаются ли изображённые на рисунке фигуры?

Решение: сначала мы должны ответить на вопрос о том, пересекаются ли прямая MN и прямая ЕF. Так как прямая бесконечна, то видим, что эти две прямые пересекаются. Теперь посмотрим, пересекаются ли отрезки MN и ЕF. Так как отрезок – это кратчайшая линия, соединяющая две точки, то наши отрезки не пересекаются. Далее посмотрим, пересекаются ли луч NM и луч FЕ. Помним, что луч имеет начало, но не имеет конца. И первой буквой обозначают начало луча. Значит, наши лучи пересекаются. И посмотрим ещё, пересекаются ли луч ЕF и луч MN. Точки Е и M – это начала наших лучей. Значит, лучи не пересекаются.

– Ребята, вы отлично справляетесь с заданиями! – с радостью сказал Электроша. – А значит, вы обязательно справитесь с моей непростой задачей.

Итак, из террариума сбежали 4 гадюки, 5 кобр и 8 гремучих змей. Длина каждой гадюки – 1 метр, каждой кобры – 1 метр 4 сантиметра, а каждой гремучей змеи – 2 метра 35 сантиметров. Сколько метров ядовитых змей сбежало из террариума?

Решение: для начала нужно перевести длину каждой змеи в одну единицу измерения. Будем переводить в сантиметры. Мы знаем, что 1 м = 100 см. Тогда длина одной гадюки равна 100 см, длина одной кобры 104 см, длина одной гремучей змеи – 235 см. Далее найдём длины всех змей каждой разновидности. Т.к. гадюк по условию сбежало 4, то длина всех гадюк в совокупности равна: 4 умножить на 100, то есть 400 см. Длина 5 кобр равна: 5 умножить на 104, то есть 520 см. И длина 8 гремучих змей равна: 8 умножить на 235, то есть 1880 см. Теперь, зная длины всех сбежавших змей, можем найти длину всех змей в совокупности. Тогда получим: 400 + 520 + 1880, то есть 2800 см. Так как в вопросе задачи сказано, что необходимо найти, сколько метров ядовитых змей сбежало из террариума, то нужно перевести 2800 см в метры. Значит, получим 28 метров.

Ответ: 28 метров ядовитых змей сбежало из террариума.