Давайте представим себе такую историю…
– Ух-ты!!! Какая красотища! – восхищался Саша.
– Саша, что такого интересного ты там увидел? – поинтересовался Паша.
– Посмотри, какие звёзды красивые!

– Да… красота! – подтвердил Паша. – А ты знаешь, что звёзды дают нам представления о простейшей геометрической фигуре?
– Как звёзды могут дать представления о геометрической фигуре? – уточнил Саша. – И что это за простейшая геометрическая фигура?
– Саша, самая простая геометрическая фигура – это точка! Вот и звёзды, когда ты на них смотришь, представляются тебе точками.
– Точно! – удивился Саша. – А я даже и не задумывался об этом! Интересно, а как точки обозначают в математике? Ведь их же как-то должны обозначать.
– Может, спросим у Электроши? – предложил Паша. – Он всё знает!
– Ребята, прежде чем мы с вами начнём говорить о геометрических фигурах, хочу, чтобы вы немного размялись и выполнили устные задания, – предложил Электроша.
– Давайте сверимся! – сказал Электроша. – Посмотрите, что у вас должно было получиться!

– Ну а теперь поговорим о точках и других геометрических фигурах, – предложил Электроша. Ребята, вы правильно заметили: если посмотреть на звёздное небо, то каждая из звёзд по отдельности будет представлять собой точку. И, кстати, точка – это простейшая геометрическая фигура. А как вы думаете, какая наука занимается изучением таких фигур? – спросил Электроша.
– Математика – ответил Саша.
– Ну, почти – перебил его Электроша. – Один из разделов математики, который изучает фигуры и их свойства, называется геометрией. Геометрия – одна из древних наук, появление и развитие которой связано, в первую очередь, с практической деятельностью людей: земледелием, строительством, желанием украсить свой быт и одежду...

– Итак, точка – это основное геометрическое понятие. В переводе с латинского языка слово «точка» означает «результат мгновенного касания».

Если вы возьмёте хорошо заточенный карандаш и прикоснётесь им к тетрадному листу, то заметите, что на листе остался след. Этот след и даёт нам представление о точке.

– Точки в математике тоже имеют свои имена – сказал Электроша.
– Имена?! – спросил Саша. – Как это забавно звучит – имена у точек.
– Точки принято обозначать большими буквами латинского алфавита: А, В, С и так далее, – продолжил Электроша. – Это и есть их имена.
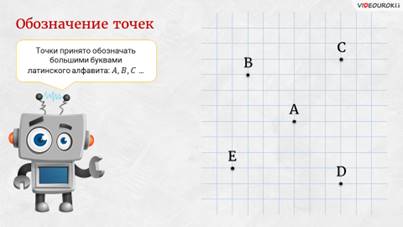
Давайте отметим на нашем листе бумаги две точки А и В. Молодцы! – похвалил ребят Электроша. – А теперь попробуйте их соединить линиями.
– Ну это же очень просто! – обрадовались мальчишки и принялись соединять точки линиями.

– Хорошо! – сказал Электроша. – Как видите эти две точки можно соединить различными линиями. А как вы думаете, какая из построенных вами линий будет самой короткой?
– Это та линия, которую я построил с помощью линейки, – уверенно произнёс Паша.
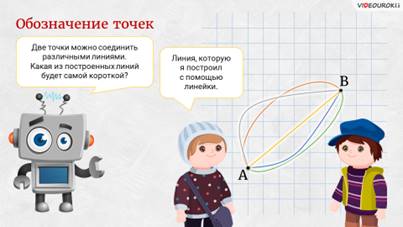
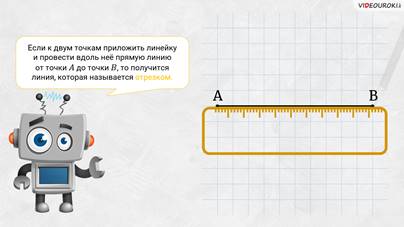
– Всё верно! – похвалил Электроша Пашу. – Если к двум точкам приложить линейку и провести вдоль неё прямую линию от точки А до точки Бэ, то получится линия, которая тоже имеет своё название. Она называется отрезком.
– А отрезок – это тоже геометрическая фигура? – решил спросить Саша.
– Да! – ответил Электроша. – Точка и отрезок – примеры геометрических фигур.
Отрезок принято обозначать именами точек, – продолжил Электроша, – то есть у нас получился отрезок АВ. Этот же отрезок можно обозначить ВА. Читают: «отрезок АВ» или «отрезок ВА». А вот сами точки А и В называют концами отрезка АВ.

– Как вы думаете, сколько отрезков можно провести через две точки? – спросил у ребят Электроша.
– Да сколько хочешь, – сказал Саша.
– А вот и неправильно, – перебил Электроша. – Любые две точки можно соединить только одним отрезком.
Запомните! Отрезок – это часть прямой линии между двумя точками, включая эти точки (концы).

– Посмотрите, – сказал Электроша, – на листке я изобразил три разных отрезка. Может, кто-то хочет их назвать?
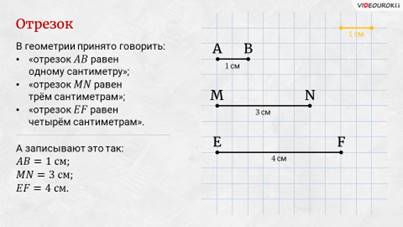
– Я назову, – сказал Паша, – отрезок АВ, отрезок MN и отрезок ЕF.
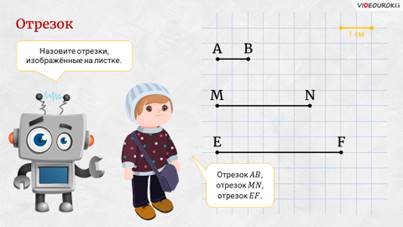
– Правильно! – похвалил Пашу Электроша. – Обратите внимание: все эти отрезки имеют разную длину. Так, отрезок АВ имеет длину 1 сантиметр. Этот же отрезок помещается в отрезке MN ровно 3 раза, а в отрезке ЕF – ровно 4 раза. Отсюда можем сделать вывод, что длина отрезка MN равна 3 сантиметрам.
– А длина отрезка ЕF – 4 сантиметра, – перебил Саша.
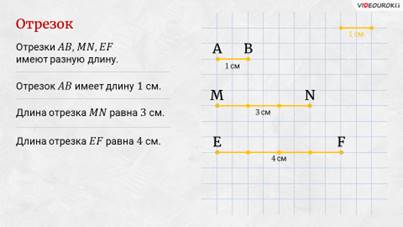
– Молодец! – похвалил Сашу Электроша. – Запомните! Длина отрезка – это расстояние между его концами.

В геометрии принято
говорить: «отрезок АB
равен одному сантиметру», «отрезок MN равен трём сантиметрам», «отрезок ЕF равен четырём сантиметрам». А записывают это
так: 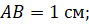
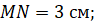
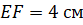 .
.
– Длины отрезков MN и ЕF, – продолжил Электроша, – мы измерили с помощью единичного отрезка, длина которого 1 сантиметр. Но для измерения отрезков можно выбрать и другие единицы измерения длины. Какие вы знаете единицы длины? – спросил Электроша у ребят.
– Существует 1 миллиметр, 1 дециметр, – сказал Саша.
– А я знаю ещё один метр, один километр, – продолжил Паша. – Кстати, большие расстояния измеряют в километрах.

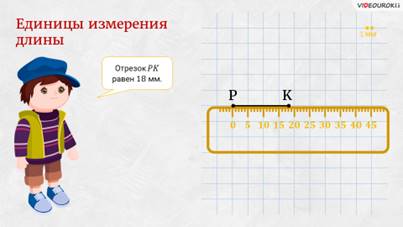
– Всё правильно! – похвалил ребят Электроша. – Посмотрите: пока вы вспоминали единицы измерения длины, я нарисовал отрезок PK. Скажите, какую длину он имеет, если измерить его, например, единичным отрезком, длина которого равна 1 миллиметр?
– Отрезок PK равен 18 миллиметрам, – сказал Саша.
– Всё верно! – похвалил Электроша. – Сделаем вывод: измерить отрезок означает подсчитать, сколько единичных отрезков в нём помещается.
– Ещё вам будет полезным узнать, каким
свойством обладает длина отрезка – продолжил Электроша.
– Давайте возьмём отрезок АB и отметим на нём некоторую точку C. Тогда можно заметить, что длина всего
отрезка АB
равна сумме длин отрезков АC и CB.
Это и есть свойство длины отрезка. А записывают его так: 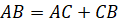 .
.

А теперь посмотрите я нарисовал два отрезка АB и CD. Давайте попробуем их совместить.
– Что вы видите? – спросил Электроша.
– Эти два отрезка полностью совпали! – воскликнули ребята.
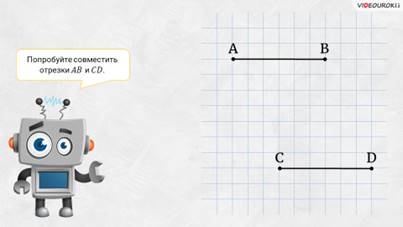
– Вы очень внимательные! – похвалил ребят Электроша. – Мы убедились, что эти два отрезка совпали при наложении. Запомните! Два отрезка называют равными, если они совпадают при наложении.

А, значит, можем сделать вывод, что отрезки АB и CD равны. Записывают это так: 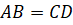 .
.
– Интересно, а эти отрезки будут иметь одинаковые длины? – спросили ребята.
– А вы померяйте их линейкой! – предложил Электроша.
– Ого! У них одинаковые длины.
– Молодцы! – похвалил ребят Электроша. – Сейчас вы сами сделали ещё один важный вывод: равные отрезки имеют равные длины.

– А как быть с неравными отрезками? – решил уточнить Паша.
– Хороший вопрос! – обрадовался Электроша. – Из двух неравных отрезков большим будем считать тот, у которого длина больше. Вот, например, на листке вы видите два отрезка ЕF и MN. Что вы можете сказать об их длинах?
– Так оно и так понятно, – сказал Саша, – отрезок ЕF больше отрезка MN.
– Или отрезок MN меньше отрезка ЕF, – продолжил Паша.

– Какие вы молодцы! – похвалил мальчиков Электроша. – Значит, мы с вами можем перейти к рассмотрению более сложной фигуры. Смотрите: если несколько отрезков соединить между собой, то получится геометрическая фигура, которую называют ломаная.
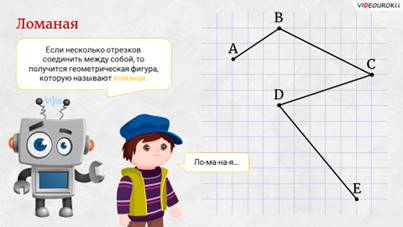
– Ло-ма-на-я! – пробормотал Саша.
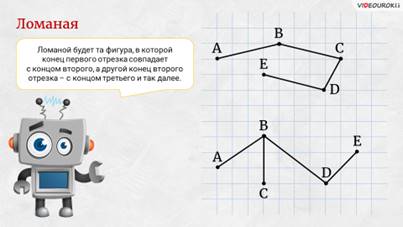
– Да, ломаная, – продолжил Электроша. – Но важно понимать, что не всегда соединённые отрезки образуют ломаную. Перед вами изображены две фигуры. Ломаной будет только та фигура, в которой конец первого отрезка совпадает с концом второго, а другой конец второго отрезка – с концом третьего и так далее. Из двух фигур, изображённых на листке, ломаной будет только первая. У второй фигуры, обратите внимание, в отрезке BC второй конец не совпадает ни с каким концом другого отрезка.
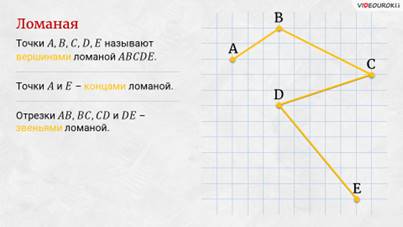
– Рассмотрим нашу ломаную подробнее, – предложил Электроша. – Точки А, B, C, D, Е называют вершинами ломаной ABCDE, точки А и Е – концами ломаной, а отрезки АB, BC, CD и DЕ – её звеньями.
– А как вы думаете, можно как-нибудь вычислить длину всей ломаной? – спросил Электроша.
– Ну, наверное, нужно измерить расстояние между первой и последней точкой ломаной? – предположил Саша.
– Нет, Саша, – сказал Электроша. – Чтобы вычислить длину всей ломаной, нужно сложить длины всех её звеньев. Давайте посчитаем, какой же будет длина нашей ломаной ABCDE.
– Ну если длина ломаной – это сумма длин всех её звеньев, – начал Паша, – то мы должны сложить 2 сантиметра, 4 сантиметра, 3 сантиметра и 5 сантиметров. Получаем, что длина нашей ломаной равна 14 сантиметрам.

– Всё правильно! – похвалил Пашу Элетроша.
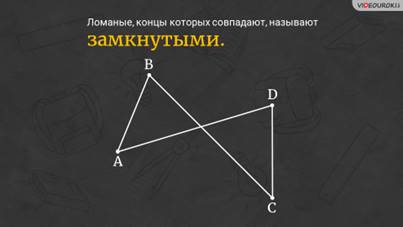
– А вот перед вами изображена ещё одна ломаная. Что особенного вы в ней заметили? – спросил у ребят Электроша.
– У неё начало и конец совпадают, – ответили мальчишки.
– Молодцы! Запомните! Ломаные, концы которых совпадают, называют замкнутыми.
– А теперь, ребята, давайте посмотрим, как вы всё поняли и выполним несколько заданий.
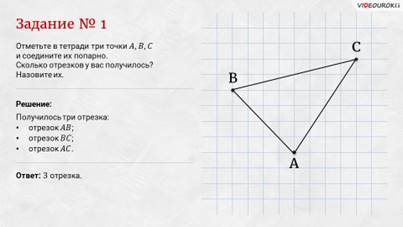
Задание первое: отметьте в тетради три точки А, B, C и соедините их попарно. Сколько отрезков у вас получилось? Назовите их.
Решение: отметим в тетради точки и соединим их попарно. Видим, что у нас получилось три отрезка: отрезок АB, отрезок BC и отрезок АC.
Следующее задание: начертите отрезок АB, длина которого 4 сантиметра 9 миллиметров. Отметьте на нём точку C так, чтобы длина отрезка CB была равна 2 сантиметрам 3 миллиметрам. Чему равна длина отрезка АC?
Решение: чертим отрезок АB длиной 4 сантиметра 9 миллиметров. Затем отмечаем на нём точку C так, чтобы выполнялось условие задание. Мы помним, что длина всего отрезка равна сумме длин составляющих его отрезков. Тогда от 4 сантиметров 9 миллиметров отнимем длину отрезка CB. Получаем, что наш отрезок АC равен 2 сантиметрам 6 миллиметрам.

И последнее задание: назовите ломаную, изображённую на рисунке, и вычислите её длину.
Решение: наша ломаная называется АBCDЕFG. А её длина равна сумме длин всех её звеньев. Складываем и видим, что длина ломаной АBCDЕFG равна 12 сантиметрам.


 Получите свидетельство
Получите свидетельство Вход
Вход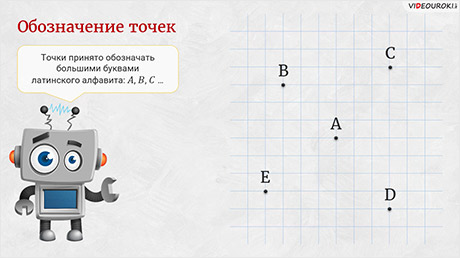



 0
0 4216
4216

